Формула полной
вероятности и формулы Байеса
Пусть
имеется полная группа попарно
несовместных событий 
, 
, …, 
с известными
вероятностями 
, 
, …, 
. Событие A может наступить только при появлении одного из
событий 
, i=1,...n,
причем известны условные вероятности 
, 
, …, 
. Найти вероятность события A по этим данным позволяет формула полной вероятности: 
.
Пример
1. Предполагается произвести два
выстрела в цель из орудия. Необходимо оценить вероятность события A:
«разрушение цели», если вероятности попадания снаряда в цель:
0-снарядов 
; 1-снаряда 
; 2-снарядов 
и вероятности разрушения цели при попадании
в нее 0 снарядов 
; 1-го снаряда 
; 2-ух снарядов 
.
Решение: Так как события 
образуют полную группу
попарно несовместных событий, то вероятность разрушения цели:
.
Пусть теперь событие A может, по-прежнему,
наступить с одним из попарно несовместных событий , , …, , образующих полную группу. Пусть в результате какого-то из испытаний событие A произошло.
Возникает вопрос, как изменятся условные вероятности событий , , …, , т.е. 
i=1,...n, в результате
наступления события A?
Ответ на этот вопрос дают формулы Байеса: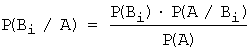 
, i=1,...n,
где 
– полная вероятность
события A.
Пример
2. По цели было произведено два
выстрела и цель, была поражена. Используя данные предыдущего примера, требуется
найти вероятности 
, 
, 
получения ровно 0, 1 и
2 попаданий.
Вероятность полного отсутствия попаданий: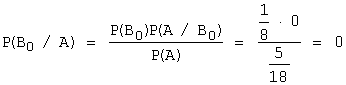 
.
Вероятности одного и двух попаданий:
; 
.
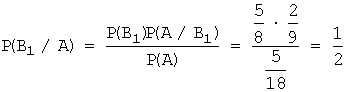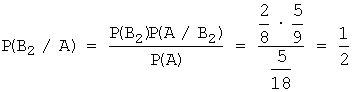Видно, что вероятности событий после
разрушения цели изменились, точнее, изменились их условные вероятности, хотя
события по-прежнему составляют полную группу.
Примеры
решения задач на тему «Формула полной вероятности. Формула Байеса»
Задача 1. Если р(А) =0,6; р(В) =0,2; р(А/В)=0,7, то чему равна
вероятность р(В/А)?
Решение.
По свойству операций над событиями: АВ =
ВА, переходя к вероятностям, получим: р(АВ) = р(ВА), используя теорему о
вероятности произведения событий, имеем:
р(АВ) = р(А)∙р(В/А) и р(ВА) =
р(В)∙р(А/В), отсюда: р(А)
∙р(В/А) = р(В) ∙р(А/В), тогда:
.
Ответ:
Р(В/А) = 0,2333.
Задача 2. Агентство по продаже недвижимости имеет четырех агентов: А, В,
С и Д. Агент А беседует с 20%, агент В - с 30%, а агенты С и Д каждый - с 25%
обратившихся в агентство клиентов. При этом 70% беседующих с агентом А, 60%
беседующих с агентом В, 65% беседующих с агентом С и 80% беседующих с агентом Д
совершают сделку.
а) Какова
вероятность того, что клиент, обратившийся в агентство, совершит сделку?
б) Клиент,
обратившийся в агентство, совершил сделку. Какова вероятность того, что это
клиент агента В?
Решение.
Обозначим:
Е –
событие, состоящее в том, что клиент, обратившийся в агентство, совершил
сделку;
А – событие, состоящее
в том, что клиент, обратившийся в агентство, беседовал с агентом А;
В
– событие, состоящее в том, что клиент, обратившийся в агентство, беседовал с
агентом В;
С
– событие, состоящее в том, что клиент, обратившийся в агентство, беседовал с
агентом С;
D – событие, состоящее в том, что клиент,
обратившийся в агентство, беседовал с агентом D.
а) Опишем процесс заключения
сделки в событиях: Е=АЕ+ВЕ+СЕ+DE, соответственно:
Р(Е) = Р(АЕ + ВЕ + СЕ + DE) = Р(АЕ) + Р(ВЕ) + Р(СЕ) + Р(DE)
= Р(А)∙Р(Е/А) + Р(В)∙Р(Е/В) + Р(С) ∙Р(Е/С) + Р(D) ∙Р(Е/D),
т.к. события АЕ, ВЕ, СЕ и DE – несовместные.
Но: Р(А)=0,2; Р(В)=0,3; Р(С)=0,25 и Р(D)= 0,25;
Р(Е/А)=0,7;Р(Е/В)=0,6;Р(Е/С)=0,65 и Р(Е/D)=0,8;
Получим: Р(Е)=0,2∙0,7+0,3∙0,6+0,25∙0,65+
0,25∙0,8=0,6825.
б) Поскольку
события А, В, С, D – гипотезы развития процесса Е, то
используя формулу Байеса, получим: 
.
Ответ:
а) Р(Е) = 0,6825; б) Р(В/Е) =
0,2637.
Задача 3. Отдел фирмы, занимающийся рекламой производимого фирмой товара,
сделал опрос большого числа жителей города. Выяснилось, что 20% опрошенных
видели рекламу товара фирмы только по телевизору, 30% видели рекламу только в
газетах, 15% видели рекламу и в газетах, и по телевизору, 35% рекламу товара не
видели. Среди тех, кто видел рекламу только по телевизору, 10% приобрели товар
фирмы; среди тех, кто видел рекламу только в газетах, товар фирмы приобрели 6%;
среди тех, кто видел рекламу и по телевизору, и в газетах, покупки сделали 15%;
из тех, кто рекламу вообще не видел, покупку сделал 1%. Определить вероятность
того, что:
а) произвольный
житель купит товар данной фирмы;
б) человек,
купивший товар фирмы, видел ее рекламу только по телевизору.
Решение.
Обозначим:
А – событие,
состоящее в том, что произвольный житель купит товар данной фирмы;
В
– событие, состоящее в том, что произвольный житель видел рекламу товара фирмы
только по телевизору;
С
– событие, состоящее в том, что произвольный житель видел рекламу товара фирмы
только в газетах;
D – событие, состоящее в том, что произвольный житель видел
рекламу товара фирмы по телевизору и в газетах;
Е
– событие, состоящее в том, что произвольный житель рекламу товара фирмы не
видел.
а)Опишем процесс
покупки товара произвольным жителем в событиях: А = ВА + СА + +DА + ЕА, соответственно:
Р(А) = Р(ВА + СА + DА
+ EА) = Р(ВА) + Р(СА) + +Р(DА)
+ Р(EА) = Р(В)∙Р(А/В) + Р(С)∙Р(А/С) + +Р(D)∙Р(A/D) + Р(Е)∙Р(А/Е), т.к. события ВА, СА, DA и ЕА – несовместные.
Но: Р(В)=0,2; Р(С)=0,3; Р(D)=0,15 и Р(Е)=0,35; Р(А/В)=0,1; Р(А/С)=0,06; Р(А/D)=0,15 и Р(А/Е)= 0,01;
Получим: Р(А)=0,2∙0,1+0,3∙0,06+0,15∙0,15+
+0,35∙0,01=0,064.
б) Поскольку
события В, С, D, Е – гипотезы развития процесса А, то
используя формулу Байеса, получим: 
.
Ответ:а) Р(A)
= 0,064; б) Р(В/A)
= 0,3125.
Задача 4. Известны результаты тестирования студентов, поступивших в
университет в данном учебном году: от 81 до 100 баллов набрали 30% поступивших,
от 61 до 80 баллов - 45%, от 40 до 60 баллов -25%. Абитуриенты, набравшие менее
40 баллов, в университет не принимались. По опыту предыдущих лет вероятность
того, что студенты, набравшие более 80 баллов на вступительном тестировании,
будут иметь академические задолженности по результатам первой сессии,
составляет 0,03; набравшие от 61 до 80 баллов могут иметь задолженности за
первую сессию с вероятностью 0,07; набравшие от 40 до 60 баллов - с вероятностью
0,1.
а) Каков ожидаемый
процент задолженников в первой сессии?
б) Какова доля
задолженников среди студентов, набравших на вступительном тесте более 80
баллов?
Решение.
Обозначим:
А – событие,
состоящее в том, что студент станет задолженником в первой сессии;
В
– событие, состоящее в том, что студент при поступлении набрал от 81 до 100
баллов;
С
– событие, состоящее в том, что студент при поступлении набрал от 61 до 80
баллов;
D – событие, состоящее в том, что студент при поступлении набрал
от 40 до 60 баллов;
а) Опишем событие
А: А = ВА + СА + DА, соответственно:
Р(А) = Р(ВА + СА + DА)
= Р(ВА) + Р(СА) + Р(DА)= = Р(В)∙Р(А/В) + Р(С)∙Р(А/С)
+ Р(D)∙Р(A/D), т.к. события ВА, СА и DA – несовместные.
Но: Р(В) = 0,3;
Р(С) = 0,45; Р(D) = 0,25;
Р(А/В) = 0,03;
Р(А/С) = 0,07; Р(А/D) = 0,1;
Получим: Р(А) = 0,3∙0,03 + 0,45∙0,07 +
+ 0,25∙0,1 =
0,0655 (или 6,55%).
б) Поскольку
события В, С, D – гипотезы для события А, то используя
формулу Байеса, получим: 
.
Ответ:
а) ожидаемый процент задолженников в первой сессии составляет
6,55%; б) доля задолженников среди
студентов, набравших на вступительном тесте более 80 баллов составит 13,74%.
Задача 5. Имеются два черных ящика. В первом находятся 2 белых, 1 синий и
3 черных шара; во втором - 2 белых, 2 синих и 2 черных шара. Из первого ящика
случайным образом перекладывают во второй 1 шар, после чего из второго ящика
опять же случайным образом вынут 1 шар.
а) Какова
вероятность, что этот шар белый?
б) Какова
вероятность того, что из первого ящика во второй был переложен синий шар, если
шар, вынутый из второго ящика, оказался белым?
Решение.
Обозначим:
А – событие,
состоящее в том, что шар, вынутый из второго ящика - белый;
В
– событие, состоящее в том, что шар, переложенный из первого ящика - белый;
С
– событие, состоящее в том, что шар, переложенный из первого ящика - синий;
D – событие, состоящее в том, что шар, переложенный из первого
ящика - черный;
а) Опишем событие
А: А = ВА + СА + DА, соответственно:
Р(А) = Р(ВА + СА + DА)
= Р(ВА) + Р(СА) + Р(DА)= = Р(В)∙Р(А/В) + Р(С)∙Р(А/С)
+ Р(D)∙Р(A/D), т.к. события ВА, СА и DA – несовместные.
Но: Р(В) = 
; Р(С) = 
; Р(D) = 
;Р(А/В) = 
; Р(А/С) = 
; Р(А/D) = ;
Получим:
Р(А) = 
.
б) Поскольку
события В, С, D – гипотезы для события А, то используя
формулу Байеса, получим: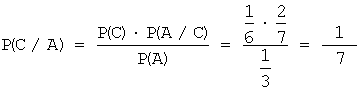 
.
Ответ:
а) Р(А) = 
; б) Р(С/А) = 
.
Задача 6. Фирма изготавливает приборы в двух вариантах: обычные и
повышенного класса точности. К отправке подготовлены 2 партии приборов (каждая
своему заказчику). В первой - 20 обычных приборов и 10 приборов повышенного
класса, во второй - 10 обычных и 24 повышенного класса точности. В последний
момент обнаружилось, что во второй партии должно быть не менее 35 приборов.
Поэтому из первой партии переложили во вторую один прибор (неизвестно, какого
класса точности). По получении груза второй заказчик случайным образом берет
один прибор. Какова вероятность, что это будет обычный прибор?
Решение.
Обозначим:
А – событие,
состоящее в том, что по получении груза второй заказчик случайным образом
возьмет обычный прибор;
В
– событие, состоящее в том, что прибор, переложенный из первой партии -
обычный;
С
– событие, состоящее в том, что прибор, переложенный из первой партии –
повышенного класса;
Опишем событие А:
А=ВА+СА, соответственно:
Р(А) = Р(ВА+СА) = Р(ВА)+Р(СА) = Р(В)∙Р(А/В)+
+Р(С)∙Р(А/С), т.к. события ВА и
СА – несовместные.
Но: Р(В)=
; Р(С)=
; Р(А/В)=
; Р(А/С)=
;
Получим:
Р(А) = 
.
Ответ:
Р(А) = 0,3048.
Задача 7. Предположим, что по уровню риска невозврата кредита банк делит
выданные кредиты на 3 категории: А - хорошие, В -среднего риска, С - плохие.
Хороший кредит в 90% случаев возвращают в срок, средний возвращают в срок в 70%
случаев, плохой - в 40% случаев. 60% выданных банком кредитов хорошие, 30% -
средние и 10% - плохие.
а) Какова
вероятность того, что случайным образом выбранный из списка кредит будет
уплачен вовремя?
б) Какова доля
хороших кредитов среди возвращаемых в срок?
Решение.
Обозначим:
А – событие,
состоящее в том, что случайным образом выбранный из списка кредит будет уплачен
вовремя;
В
– событие, состоящее в том, что случайным образом выбранный из списка кредит -
хороший;
С
– событие, состоящее в том, что случайным образом выбранный из списка кредит –
среднего риска;
D – событие, состоящее в том, что случайным образом выбранный из
списка кредит - плохой;
а) Опишем событие
А: А = ВА + СА + DА, соответственно:
Р(А) = Р(ВА + СА + DА)
= Р(ВА) + Р(СА) + Р(DА)= = Р(В)∙Р(А/В) + Р(С)∙Р(А/С)
+ Р(D)∙Р(A/D), т.к. события ВА, СА и DA – несовместные.
Но: Р(В) = 0,6;
Р(С) = 0,3; Р(D) = 0,1;
Р(А/В) = 0,9; Р(А/С) = 0,7; Р(А/D)
= 0,4;
Получим:
Р(А)=0,6∙0,9+0,3∙0,7+0,1∙0,4 = 0,79.
б) Поскольку
события В, С, D – гипотезы для события А, то используя
формулу Байеса, получим: 
.
Ответ:
а) Р(А) = 0,79; б) доля
хороших кредитов среди возвращаемых в срок составит 68,35%.
Задача 8. У шоссе находится кафе "Макдоналдс". Количество
легковых и грузовых автомашин, проезжающих по этой дороге, относится как 4:1. В
среднем 7% водителей грузовых машин и 1% водителей легковых машин
останавливаются здесь перекусить. Какова вероятность того, что зашедший поесть
водитель является водителем легкового автомобиля?
Решение.
Обозначим:
А – событие,
состоящее в том, что произвольный водитель зайдет перекусить в кафе;
В
– событие, состоящее в том, что зашедший
в кафе водитель – водитель грузового автомобиля;
С
– событие, состоящее в том, что зашедший
в кафе водитель – водитель легкового автомобиля;
Опишем событие А в
зависимости от событий В и С: А = ВА + СА, соответственно:
Р(А) = Р(ВА + СА) = Р(ВА) + Р(СА) =
= Р(В)∙Р(А/В) + Р(С)∙Р(А/С),
т.к. события ВА и СА – несовместные.
Поскольку
соотношение водителей легковых и грузовых автомобилей 4:1, то:
Р(В) = 0,2; Р(С) = 0,8; и
Р(А/В) = 0,07; Р(А/С) = 0,01 – по условию;
Получим:
Р(А) = 0,8∙0,01 + 0,2∙0,07 = 0,022.
Поскольку
события В и С – гипотезы для события А, то используя формулу Байеса, получим:
.
Ответ:
Р(С/А) = 0,364.
Задача 9. Имеется урна, в которой 7 белых и 3 черных шаров. Вынимают
наугад два шара и перекрашиваются в черный цвет и кладут обратно в урну. Затем
вынимают один шар. Он - белый. Какова вероятность того, что оба перекрашенных
шара были белыми?
Решение.
Обозначим:
А – событие,
состоящее в том, что шар, вынутый из ящика после перекрашивания - белый;
В
– событие, состоящее в том, что вынули наугад и перекрасили два белых шара;
С
– событие, состоящее в том, что вынули наугад и перекрасили один белый и один
черный шар;
D – событие, состоящее в том, что вынули наугад и перекрасили два
черных шара;
Опишем событие А: А
= ВА + СА + DА, соответственно:
Р(А) = Р(ВА + СА + DА)
= Р(ВА) + Р(СА) + Р(DА)= = Р(В)∙Р(А/В) + Р(С)∙Р(А/С)
+ Р(D)∙Р(A/D), т.к. события ВА, СА и DA – несовместные.
Но: Р(В)=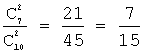
;
Р(С) =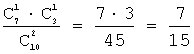 
; Р(D) = 
;
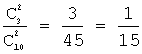Р(А/В) = 
; Р(А/С)=
; Р(А/D) = 
;
Получим: Р(А) = 
.
Поскольку события В, С, D – гипотезы для события А, то используя формулу Байеса, получим:
.
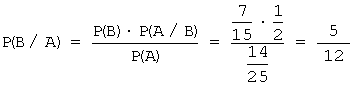Ответ:
Р(B/А) = 
.
Задача 10. По цели выпускают последовательно три ракеты. Первая поражает
цель с вероятностью 0,8; вторая - с вероятностью 0,7; и третья - с вероятностью
0,6. Известно, что цель поражена одной ракетой. Какова вероятность, что цель
поражена второй ракетой?
Решение.
Обозначим:
А – событие,
состоящее в том, что цель поражена одной ракетой;
В
– событие, состоящее в том, что цель поражена первой ракетой;
– событие, состоящее в
том, что цель не поражена первой ракетой;
С – событие,
состоящее в том, что цель поражена второй ракетой;
– событие, состоящее в
том, что цель не поражена второй ракетой;
D – событие, состоящее в том, что цель поражена третьей ракетой;
– событие, состоящее в
том, что цель не поражена третьей ракетой;
Опишем событие А:
, соответственно:
Р(А)=Р(
) = Р(
)+ + Р(
) + Р(
) = Р(В)∙Р()∙Р() +
+ Р()∙Р(С)∙Р() + Р()∙Р()∙Р(D), т.к. события 
– несовместные, а
события В, С, D - независимые.
Получим:
Р(А) = 0,8∙0,3∙0,4 + 0,2∙0,7∙0,4 +
+ 0,2∙0,3∙0,6 = 0,188.
Поскольку событие
А реализовалось, то используя формулу
Байеса, получим:
.
Ответ:
Вероятность того, что цель поражена второй ракетой Р(С/А) = 0,2979.
Задача 11. В мешок, содержащий
два шара неизвестного цвета, опущен белый шар. После встряхивания извлечен один
шар. Найти вероятность того, что извлеченный шар окажется белым, если
равновозможны любые предположения о цвете двух шаров, находившихся в мешке.
Решение:
Пусть А – событие извлечения белого
шара. Построим предположения о первоначальном составе шаров:
В1 – белых шаров нет; В2 –
один белый шар из двух; В3 – оба шара белые.
Так как гипотезы В1, В2
и В3 по условию равновероятны, то 
.
‑
если в мешке первоначально не было белых шаров, то 
, так как только одно событие из трех благоприятно;
‑
в мешке уже был один белый шар, следовательно 
, так как уже два события из трех благоприятны;
‑
в мешке оба шара были белые: 
.
Искомую вероятность того, что будет
извлечен белый шар, найдем по формуле полной вероятности:
.
Задача 12. Два автомата
производят одинаковые детали. Производительность первого автомата в два раза
больше производительности второго. Вероятность производства отличной детали у
первого автомата равна 0,60, а у второго 0,84. Наудачу взятая для проверки
деталь оказалась отличного качества. Найти вероятность того, что эта деталь
произведена первым автоматом.
Решение:
Пусть А – событие: деталь отличного качества. Можно выдвинуть две гипотезы:
В1 – деталь произведена первым
автоматом. Тогда 
, так как этот автомат производит, по условию, деталей в два
раза больше второго.
В2 – деталь изготовлена вторым
автоматом, причем 
.
Условные вероятности того, что деталь
произведена первым автоматом, по условию: 
, а вторым – 
.
Вероятность того, что наудачу взятая деталь
окажется отличного качества, по формуле полной вероятности:
.
Искомая вероятность того, что взятая деталь
изготовлена первым автоматом, по формуле Байеса: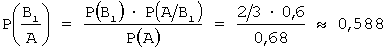 
.