ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Определение. Дифференциальным
уравнением называется уравнение, связывающее искомую функцию одной или
нескольких переменных, сами переменные и производные этой функции различных
порядков.
Рассмотрим
некоторые примеры:
1)![]() =-kx
=-kx
–
дифференциальное
уравнение радиоактивного распада (k - постоянная распада, x - количество неразложившегося вещества в момент
времени t, скорость распада dx/dt
пропорциональна количеству распадающегося вещества).
2)![]() =mx
=mx
– дифференциальное
уравнение, описывающее увеличение числа
бактерий, в предположении, что скорость их размножения dx/dt
пропорциональна (с коэффициентом m) наличному
числу бактерий x.
3)![]() +
+![]() +
+![]() =4pr
=4pr
– дифференциальное
уравнение Пуассона, которому
удовлетворяет, например,![]() потенциал u(x;y;z)
электростатического поля, r(x;y;z)-плотность
зарядов.
потенциал u(x;y;z)
электростатического поля, r(x;y;z)-плотность
зарядов.
4)
– дифференциальное уравнение движения точки массы m под влиянием силы ![]() , где
, где ![]() -радиус-вектор точки,
-радиус-вектор точки,
![]() – её скорость,
– её скорость, ![]() – ускорение ( 2-ой закон Ньютона).
– ускорение ( 2-ой закон Ньютона).
5) mx"
= - cx
– дифференциальное
уравнение движения груза массы m на пружине под действием силы упругости F = -cx (c - коэффициент жёсткости пружины).
6)lj" = -g·sinj
– дифференциальное
уравнение колебаний математического
маятника; lj” = - gj – для малых колебаний (sinj » j).
7) y" =
![]()
– дифференциальное
уравнение свободного полёта ракеты,
удаляющейся от Земли под влиянием силы F = 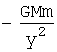 ,
,
где
G - гравитационная постоянная, M - масса Земли.
Функция, удовлетворяющая дифференциальному уравнению, т.е.
обращающая его в тождество, называется интегралом (или решением) этого
уравнения, а ее график – интегральной кривой.
Задача нахождения такой функции называется
интегрированием (или решением) дифференциального уравнения.
Если искомая функция зависит только от
одного аргумента, то дифференциальное уравнение называется обыкновенным. Если
исходная функция зависит от нескольких аргументов, а само дифференциальное
уравнение содержит частные производные – то уравнением в частных производных.
Порядком дифференциального уравнения называется порядок высшей
производной, содержащейся в этом уравнении.
Так, уравнение ![]() - второго порядка;
- второго порядка;
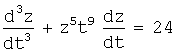 - третьего порядка;
- третьего порядка;
![]() - первого порядка.
- первого порядка.
Определение. Обыкновенным дифференциальным
уравнением n-го порядка называется уравнение вида F (x,y,y’,y”,…,y(n))=0, связывающее независимую переменную x,
неизвестную функцию y(x) и её производные.
Это уравнение часто записывают в виде,
разрешённом относительно наивысшей производной
y(n)=f(x,y,y’,y”…y(n-1)), а также в виде F(x,y,dx,dy,d2y,…
dny)=0.
Определение. Решением дифференциального уравнения F(x,y,y’,y”… y(n))=0 называется всякая функция y=y(x), которая при
подстановке в уравнение вместе со своими
производными, обращает его в тождество.
Следует отменить, что в решении
дифференциального уравнения содержится такое количество произвольных
постоянных, каков порядок уравнения. Таким образом, решение дифференциального
уравнения n-го порядка содержит n произвольных констант, т.е.
y=y(x,С1,С2 … Сn)
или Ф(x,y,С1,С2
… Сn)=0.
Решение (интеграл) дифференциального уравнения n-го порядка, зависящее от n произвольных
независимых постоянных, называется общим решением (общим интегралом) этого уравнения.
Решение (интеграл), полученное при
конкретных числовых значениях этих постоянных, называется частным решением (частным интегралом) этого уравнения.
В
большинстве задач, связанных с нахождением решения дифференциального уравнения
задают дополнительные (начальные) условия:
![]() ;
; ![]() ;
; ![]() ; ... ;
; ... ; ![]() .
.
Задача нахождения частного решения
(частного интеграла) дифференциального уравнения, удовлетворяющего начальным
условиям, называется задачей Коши.
Геометрически каждому частному решению дифференциального уравнения
соответствует своя интегральная кривая, а общему интегралу – совокупность
(семейство) интегральных кривых.
Например, дифференциальное
уравнение радиоактивного распада x'=-kx имеет
решение x=Ce-kt,
где C-произвольная постоянная (единственная, т.к. уравнение
1-го порядка). Однако, это уравнение не полностью
определяет закон распада x=x(t), т.к. надо знать
количество распадающегося вещества x0 в некоторой начальный
момент t0,
т.е. начальное условие x0=x(t0). Тогда решение x(t)=x0e-k(t-t0).
Дифференциальное уравнение 2-го порядка вида
x”+ω2x=0 (ω=const)
обычно называют уравнением гармонических колебаний. Его общее решение имеет вид
x(t)=C1sin(ωt+C2),
C1; C2 - две произвольные
постоянные (амплитуда и фаза соответственно).
Дифференциальные
уравнения 1-го порядка.
Согласно
определению дифференциального
уравнения 1-го порядка - это уравнение
вида
F(x;y;y’)=0 или y’=f(x;y), если удаётся разрешить
относительно y’.
Решением будет являться семейством функций y=y(x;С), которые при подстановке
в уравнение обращают его в тождество.
Задача Коши по отысканию частного решения дифференциального
уравнения, удовлетворяющего начальным условиям,
записывается в виде:
y’=f(x;y),y(x0)=y0.
Общим решением дифференциального уравнения
1-го порядка ![]() называется функция
называется функция ![]() , такая что
, такая что
а) она обращает дифференциальное уравнение
в тождество при любом значении ![]() ;
;
б) при заданном начальном условии ![]() существует
единственное
существует
единственное ![]() , такое что
, такое что ![]()
![]() удовлетворяет начальному условию;
удовлетворяет начальному условию; ![]()
![]() называется частным
решением.
называется частным
решением.
Теорема($!решения). ![]() Если
в уравнении y'=f(x;y) функция f(x;y) и её производная ∂f/∂y непрерывны в
некоторой области, содержащей точку (x0;y0), то существует и при том единственное решение этого уравнения,
удовлетворяющее начальному условию y(x0)=y0.
Если
в уравнении y'=f(x;y) функция f(x;y) и её производная ∂f/∂y непрерывны в
некоторой области, содержащей точку (x0;y0), то существует и при том единственное решение этого уравнения,
удовлетворяющее начальному условию y(x0)=y0.
Геометрический
смысл теоремы заключается в том, что при выполнении указанных условий $! функция у = у(x), удовлетворяющая дифференциальному уравнению y'=f(x;y), график которой проходит через точку (x0;y0).
Таким образом, общее решение задаёт семейство
интегральных кривых, а решение задачи Коши определяет единственную кривую из
этого семейства.
Заметим, что теорема даёт достаточные
условия, которые не являются необходимыми.
Например:
y'=1/y2.
Здесь f(x;y)=1/y2 и ∂f/∂y = -2/y3 разрывны на оси Ox,
в точках (x0;0), но через
каждую точку оси Ox проходит единственная интегральная
кривая ![]() .
.
Дифференциальные
уравнения с разделяющимися переменными
Самые простые дифференциальные уравнения - с разделяющимися переменными.
Уравнение первого порядка ![]() называется уравнением
с разделяющимися переменными, если функции
называется уравнением
с разделяющимися переменными, если функции ![]() и
и ![]() разлагаются на
множители, зависящие каждый от одной переменной:
разлагаются на
множители, зависящие каждый от одной переменной: ![]() .
.
В таком уравнении путем деления его членов
на ![]() , переменные разделяются:
, переменные разделяются: 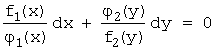 .
.
После разделения переменных каждый член
уравнения будет зависеть только от одной
переменной, и общий интеграл уравнения
находится интегрированием: 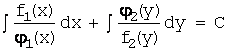 .
.
Заметим, что при делении могут быть
потеряны решения уравнения ![]() . Если они не войдут в общий интеграл, их надо указывать
отдельно, так называемые особые решения.
. Если они не войдут в общий интеграл, их надо указывать
отдельно, так называемые особые решения.
Примеры решения задач.
1.Найти общий интеграл
следующего уравнения:
![]()
Решение. Разделим
переменные в данном уравнении, деля обе его части на ![]() :
: 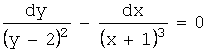 .
.
Интегрируя, получим искомый общий интеграл:
![]() , откуда
, откуда 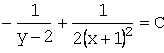 .
.
Заметим, что при делении были потеряны
решения x = -1, y
= 2, они являются особыми.
2. Решить уравнение ![]() .
.
Решение. ![]() ,
, ![]() ,
, ![]() ,
,
интегрируем обе
части полученного уравнения ![]() ,
,
откуда 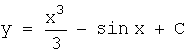 .
.
Дифференцированием
можно проверить правильность полученного результата.
3. Решить уравнение ![]() .
.
Решение.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Так как C – произвольная
постоянная, то ее можно записать в любой удобной форме.
Поэтому используем запись:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
4. Найти частное
решение уравнения ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]() .
.
Решение.
![]() ,
, ![]() .
.
Интегрируем: ![]()
![]()
![]() .
.
По заданному начальному условию найдем
значения константы![]() :
:
![]() или
или ![]() , т.е.
, т.е.![]() = –2.
= –2.
Искомое частное решение имеет вид: ![]() .
.
Линейные
дифференциальные уравнения
Дифференциальные уравнения вида ![]() называются линейными дифференциальными
уравнениями,
называются линейными дифференциальными
уравнениями, ![]() - непрерывные функции.
- непрерывные функции.
Для решения
используют два метода:
-метод вариации
произвольной постоянной;
-метод
подстановки (Бернулли);
Суть метода
подстановки заключается в том, что решение уравнения ищут в виде
произведения двух неизвестных функций u = u(x) и v
= v(x), одна из которых (напр., v = v(x)) может быть
выбрана произвольно. Т.е. y = u∙v, тогда y¢ = u¢v+v¢u, и, подставляя y и y¢ в исходное уравнение, получаем:
y¢+p(x)∙y
= f(x) Þ u¢v+uv¢+p(x)u∙v = f(x) Þ u¢v+u×(v¢+p(x)v) = f(x).
Пользуясь тем, что
одна из неизвестных функций, например, v
= v(x), может быть выбрана произвольно, так как
только результат произведения u∙v должен удовлетворять исходному уравнению, выберем v = v(x) таким образом,
чтобы выражение в скобках равнялось нулю: v¢+p(x)∙v=0.
Таким образом,
решение исходного линейного уравнения сводится к решению системы двух
дифференциальных уравнений с разделяющимися переменными: 
Решая первое
уравнение, разделяя переменные, получим:
v¢+Р(x)∙v=0 Þ ![]() =-р(x)∙v Þ
=-р(x)∙v Þ ![]() =-р(x)dx Þ
=-р(x)dx Þ
Þ v=![]() .
.
Полагая С = 1, находим v = ![]() .
.
Далее, подставляя
найденное значение v во второе уравнение системы,
получаем u¢∙v=f(x) Þ
Þ ![]() ×
×![]() =f(x)
Þ du=f(x)
=f(x)
Þ du=f(x)![]() dx
Þ
dx
Þ
Þ u=∫f(x)![]() dx +C.
dx +C.
Т.к.y=u∙v, то y=C![]() +
+ ![]() ∫f(x)
∫f(x)![]() dx -
общее решение.
dx -
общее решение.
Заметим,
что эту формулу запоминать не следует, а при решении конкретных уравнений
целесообразно повторять вышеизложенные рассуждения.
5.Решить уравнение ![]() . Решение.
. Решение.![]()
![]()

![]()
![]()


Ответ: 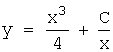 .
.
6.Найти
решение дифференциального уравнения y¢+3y = e2x,
удовлетворяющее начальным условиям y (0)=0.
Т.е. решить задачу Коши: 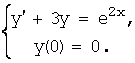
Решение: Сначала найдем общее решение уравнения.
Для этого полагаем y = u∙v Þ y¢ = u¢∙v+v¢∙u,
тогда u¢v + v¢u + 3uv = e2x
Þ
u¢v + u×(v¢ + 3v) = e2x.
Решение исходного линейного
уравнения сводится к решению системы двух дифференциальных уравнений с
разделяющимися переменными: 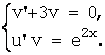
Решаем первое
уравнение системы:
v¢+3v = 0 Þ ![]() = -3v Þ
= -3v Þ ![]() = -3dx Þ v = e-3x.
= -3dx Þ v = e-3x.
Далее решаем второе уравнение:
u¢v=e2x Þ u¢e-3x = e2x Þ ![]() = e5x Þ du = e5x∙dx Þ
= e5x Þ du = e5x∙dx Þ![]() .
.
Таким образом, общее решение уравнения:
y = u∙v Þ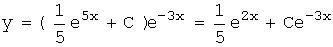 .
.
Теперь найдем частное решение.
Используя начальное условие задачи y(0)=0, вычислим соответствующее
ему значение С:
y(0)=0 Þ 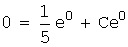 Þ
Þ
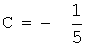 Þ
Þ
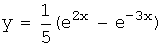 .
.
Уравнения
Я.Бернулли
Среди
различных приложений широко используются yравнения Бернулли: ![]() , n Î R.
, n Î R.
Отметим, что при n
= 1 данное уравнение становится уравнением с разделяющимися переменными, при n = 0 – это линейное уравнение.
Уравнение Бернулли можно привести к
линейному, разделив обе части на yn и введя замену
переменной по формуле:
z = y1-n, z¢= 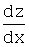 =(1-n)×y-n
=(1-n)×y-n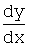 ,
,
тогда:
y¢+p(x)y = f(x)yn
Þ y-n∙y¢+p(x)y1-n = f(x) Þ
Þ ![]() +(1- n)p(x)z = (1-n)f(x).
+(1- n)p(x)z = (1-n)f(x).
Последнее уравнение является линейным дифференциальным уравнением относительно новой переменной z(x).
Заметим, что уравнение Бернулли можно решить непосредственно с помощью
подстановки y = u∙v, не сводя его предварительно к
линейному, а просто решая по аналогичному алгоритму.
7.Решить уравнение ![]() .
.
Решение: Это уравнение Бернулли.
Будем использовать подстановку y = u∙v, y¢ = u¢v+v¢u,
тогда u¢v+v¢u-![]() =-u2∙v2 Þ u¢v+u(v¢-
=-u2∙v2 Þ u¢v+u(v¢-![]() )=-u2∙v2.
)=-u2∙v2.
Решение
исходного уравнения сводится к решению
системы двух дифференциальных уравнений с разделяющимися переменными: 
Решаем первое
уравнение системы: v¢-![]() =0 Þ
=0 Þ
Þ ![]() =
= ![]() Þ
Þ ![]() =
= ![]() Þ ln v = ln x Þ v = x.
Þ ln v = ln x Þ v = x.
Далее решаем второе уравнение:
u¢v
=-u2∙v2 Þ Þ u¢= - u2∙v Þ ![]() Þ
Þ
Þ ![]() Þ
Þ 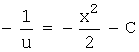 Þ
Þ 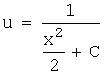 .
.
Общее решение уравнения: y = u∙v
=![]() .
.
Однородные
дифференциальные уравнения
Функция f(x;y) называется однородной
функцией нулевого измерения, если при умножении переменных x и y на произвольный множитель l¹0 значение функции не
изменяется, т.е."l ¹ 0 выполнено условие f(lx;ly) = f(x;y).
Например, функция f(x;y)=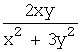 является однородной
функцией нулевого измерения, т.к.
является однородной
функцией нулевого измерения, т.к.
f(lx;ly)=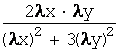 =
=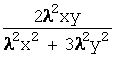 =
=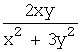 =
=
=l0×f(x;y)=f(x;y).
Однородная функция нулевого измерения всегда
может быть представлена в виде f(x;y) = ![]() .
.
Действительно, т.к. f(x;y) - однородная
функция нулевого измерения, то, выбрав в качестве множителя l
=![]() ,
,
получаем f(x;y) = f (lx;ly) = f(1;![]() ) =
) = ![]() .
.
Определение. Дифференциальное уравнение y¢=f(x;y) называется однородным, если функция
f(x;y) - однородная функция нулевого измерения.
Однородное
дифференциальное уравнение можно представить в виде y¢=![]() .
.
Однородное
дифференциальное уравнение можно привести к уравнению с разделяющимися
переменными с помощью подстановки z =![]() или y = z×x , где z - новая
функция.
или y = z×x , где z - новая
функция.
Дифференцируя
равенство y=z×x, получим: y¢=z¢x+z Þ
Þ z¢x+z =![]() Þ z¢x =
Þ z¢x =![]() -z
Þ
-z
Þ ![]() =
= ![]() -z
Þ
-z
Þ ![]() ,
,
т.е.
получили уравнение с разделенными переменными x и z.
![]() Þ z = Y(x;C) Þ
Þ z = Y(x;C) Þ
Þ ![]() = Y(x;C) Þ y = x×Y(x;C).
= Y(x;C) Þ y = x×Y(x;C).
8. Решить уравнение y¢= ![]() .
.
Решение.
Легко установить, что правая часть заданного уравнения является
однородной функцией
нулевого измерения. Следовательно, уравнение является однородным и его можно
привести к уравнению с разделяющимися переменными с помощью подстановки z =![]() или y = z×x , где z (x) - новая функция.
или y = z×x , где z (x) - новая функция.
Дифференцируя
равенство y = z×x, получим:
y¢ = z¢x+z. Тогда заданное уравнение примет вид
z¢x
+ z = 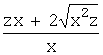 или z¢×x
+ z = z + 2
или z¢×x
+ z = z + 2![]() ,
,
z¢×x = 2![]() ,
, ![]() .
.
Полученное
уравнение с разделёнными переменными. Интегрируя, получим:
![]() ,
, ![]() ,
, ![]() .
.
Так
как z =![]() , то получаем
, то получаем ![]()
или
![]() - общее решение заданного
уравнения.
- общее решение заданного
уравнения.
Функция f(x;y) называется однородной функцией n-го измерения, если "l ¹ 0 выполнено условие f(lx;ly)=ln ×f(x;y).
Наример, f(x;y)=x2+2xy-y2 –однородная функция
2-го измерения, т.к. f(lx; ly) = l2x2 + 2lxly - l2y2 = l2 (x2-2xy-y2) = l2×f(x; y).
Дифференциальное уравнение первого
порядка M(x,y)dx + N(x,y)dy = 0
будет однородным, если коэффициенты при
дифференциалах dx и dy,
т.е. функции
M
(x,y) и N
(x,y), являются функциями одного и того же
измерения.
9. Решить уравнение ![]() .
.
Решение. Коэффициенты при дифференциалах dx и dy,
т.е. функции M(x,y) = ![]() и N(x,y) =
и N(x,y) = ![]()
являются функциями одного и того же
измерения (второго). Следовательно, уравнение является однородным и его можно
привести к уравнению с разделяющимися переменными с помощью подстановки z=![]() или y=z×x, где z(x) - новая функция.
или y=z×x, где z(x) - новая функция.
Дифференцируя равенство y=z×x, получим: y¢=z¢x+z.
Запишем уравнение ![]() в виде y¢=
в виде y¢= 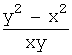 .
.
Тогда
z¢x+z = 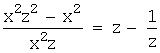 Þ
Þ
Þ z¢x =![]() Þ zdz =
Þ zdz =![]() .
.
Интегрируя,
будем иметь: 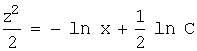 ,
, ![]() .
.
Так
как z =![]() , то получаем
, то получаем ![]()
![]() - общий интеграл
заданного уравнения.
- общий интеграл
заданного уравнения.
Дифференциальные
уравнения 2-го порядка
Согласно
определению дифференцируемым уравнением 2-го
порядка называется уравнение вида F(x;y;y’;y”)=0 или в виде, разрешенном относительно y”: y”=f(x;y;y’).
Начальные условия при х=х0
задают так:
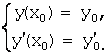
Задача Коши по отысканию частного решения дифференциального
уравнения, удовлетворяющего начальным условиям,
записывается в виде:

![]() Теорема($!решения). Eсли в уравнении y”=f(x;y;y’) функция f(x;y;y’) и ее частные
производные
Теорема($!решения). Eсли в уравнении y”=f(x;y;y’) функция f(x;y;y’) и ее частные
производные ![]() непрерывны в некоторой
области,
непрерывны в некоторой
области,
содержащей точку ![]() , то существует и при том единственное решение у=у(х),
удовлетворяющее начальным условиям
, то существует и при том единственное решение у=у(х),
удовлетворяющее начальным условиям 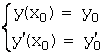 .
.
Геометрический смысл теоремы заключается в
том, что ![]() ! функция у=у(х), удовлетворяющая дифференциальному уравнению y”=f(x;y;y’), график которой проходит через заданную
точку (х0;у0) с заданным тангенсом угла наклона
касательной к этой кривой, равным
! функция у=у(х), удовлетворяющая дифференциальному уравнению y”=f(x;y;y’), график которой проходит через заданную
точку (х0;у0) с заданным тангенсом угла наклона
касательной к этой кривой, равным ![]() .
.
Общим решением дифференциального
уравнения 2-го порядка ![]() называется функция
называется функция ![]() , такая что
, такая что
а)она обращает
дифференциальное уравнение в тождество при любых значениях ![]() ;
;
б)при заданных
начальных условиях ![]() существует
единственная пара
существует
единственная пара ![]() , такая что
, такая что ![]() удовлетворяет
начальным условиям (предполагается, что
удовлетворяет
начальным условиям (предполагается, что ![]() принадлежат области, в
которой выполняются условия теоремы существования и единственности решения);
принадлежат области, в
которой выполняются условия теоремы существования и единственности решения);
Если общее решение получено в неявном виде, то его называют
общим интегралом:Ф(х;у;С1;С2)=0.
Частным решением называют решение,
полученное из общего при конкретных значениях произвольных постоянных С1; С2.
Пример
из механики.
Рассмотрим уже упомянутую
задачу о движении ракеты:y”=![]() (или
(или 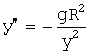 )
)
- дифференциальное уравнение свободного полёта ракеты, удаляющейся от Земли под
влиянием силы F=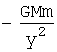 ,
,
где G - гравитационная постоянная, M - масса Земли, g – постоянная тяготения, R – радиус Земли.
Пусть
ракета стартует с поверхности Земли (отметим, что почти горизонтально), т.е.
первое начальное условие, задающее начальное положение ракеты, имеет вид у(0)=R, т.е. у=R, при t=0. Второе начальное условие – скорость в начальный
момент времени ![]() при t=0. Покажем, как решение
уравнения, т.е. траектория движения ракеты, зависит от этого начального
условия. В механике рассматривают две начальные скорости:
при t=0. Покажем, как решение
уравнения, т.е. траектория движения ракеты, зависит от этого начального
условия. В механике рассматривают две начальные скорости:
![]()
![]() 7,9 км/с – 1-ая космическая скорость,
7,9 км/с – 1-ая космическая скорость,
![]()
![]() 11,2 км/с–2-ая космическая скорость.
11,2 км/с–2-ая космическая скорость.
Если V0<V01, то ракета упадет на Землю.
Если V0=V01, то ракета станет
искусственным спутником Земли и будет двигаться по круговой орбите.
При V01<V0<V02 траекторией движения ракеты
будет эллипс. V0=V02 –
наименьшая начальная скорость, при которой ракета может покинуть поле тяготения
Земли и улететь по параболе.
Если V0>V02, то ракета покидает поле
тяготения земли по гиперболе.
Из приведенного примера ясно, что
для решения задачи Коши дифференциального уравнения 2го порядка,
нужно задавать 2 начальных условия у(х0)=у0
и ![]() , которые в механике соответствуют начальному положению тела у(0) и его начальной скорости V0.
, которые в механике соответствуют начальному положению тела у(0) и его начальной скорости V0.
Дифференциальные
уравнения, допускающие понижение порядка
Ряд дифференциальных уравнений 2-го порядка с помощью соответсвующих замен можно привести к уравнениям 1-го
порядка, т.е. понизить порядок.
Дифференциальные уравнения, допускающие
понижение порядка, - это уравнения вида:
а)y”![]()
б)y”![]() ’),
’),
в)y”=![]() ’);
’);
порядок понижается путём замены: y’(x)=р(x), y”(x)=рx’(x) в случае а) и б);
или: y’(x)=р(y), y”(x)= рy’(y)∙р(y)
в случае в):
а) уравнения вида ![]() f(x).
f(x).
Особенностью таких уравнений
является то, что они не содержат в явной форме у и ![]() .Решение основано на поэтапном интегрировании y”=f(x):
.Решение основано на поэтапном интегрировании y”=f(x):
![]()
![]()
![]() .
.
10. Решить
уравнение: ![]() .
.
Решение:![]() ,
,![]() ,
,
![]() -общее
решение.
-общее
решение.
Найдем частное решение,
соответствующее данным начальным условиям.
![]() ,
, ![]() ,
,
![]() - частное
решение.
- частное
решение.
11.Решить
задачу Коши:
![]() ,
, ![]() .
.
Решение.
Два раза последовательно проинтегрировав, получим общее решение: 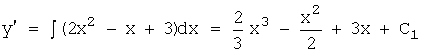 ,
,
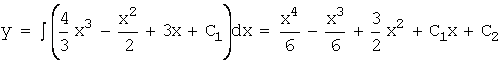 .
.
Подставим начальные условия, получим
значения констант:
![]()
Следовательно, искомое частное решение
имеет вид: 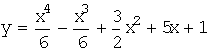 .
.
Замечание.
Уравнения вида у(n)=f(x) решаются аналогично.
12. Решить уравнение: ![]() .
.
Решение: ![]() ,
,
![]() ,
,
![]() -общее
решение.
-общее
решение.
б)yравнения вида ![]() .
.
Особенность данных уравнений -
отсутствие в явной форме искомой функции у.
Решение основано на применении
постановки вида ![]() тогда
тогда ![]() ,
,
и уравнение приводится к
уравнению первого порядка относительно новой переменной р:![]()
![]() .
.
Решая последнее находят р(х;С1),
далее интегрируя: ![]() .
.
13.
Решить уравнение: ![]() .
.
Решение: обозначим ![]() , тогда
, тогда ![]() и
и
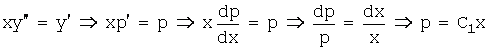 .
.
Далее ![]() - общее решение.
- общее решение.![]()
14. Найти решение уравнения:
![]()
Решение.
Заменой
y’=р(x) понизим порядок:
y”=р’(x),![]() ,
, 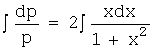 ,
,
![]() ,
,![]() ,
,![]() ,
,
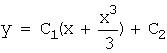 -это общее решение.
-это общее решение.
Найдём
частное решение: y(1)=0![]()
![]() ,
,
y’(1)=1 ![]() ,
,
частное решение: 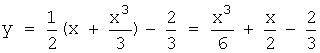 .
.
Замечание.
Уравнения вида ![]() , не содержащие искомой функции у, тоже допускают понижение
порядка, если за новую неизвестную функцию взять низшую из производных данного
уравнения, т.е.
, не содержащие искомой функции у, тоже допускают понижение
порядка, если за новую неизвестную функцию взять низшую из производных данного
уравнения, т.е.![]()
![]() .
. ![]()
Тогда получим уравнение ![]() , порядок которого понизился на r-единиц.
, порядок которого понизился на r-единиц.
15. Решить
уравнение:![]()
Решение: сделаем замену ![]()

![]() -
-
- это общее решение.
в)yравнения вида ![]() .
.
Такие
уравнения не содержат в явной форме независимую переменную х. Для решения
используют подстановку: ![]() ,
,
тогда по правилу дифференцирования сложной
функции ![]()
и
![]() -
-
это
уравнение первого порядка.
Интегрируя
его, найдем р=р(у;С1),
далее
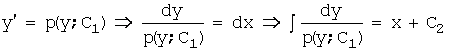 .
.
16.Найти общее решение уравнения ![]() .
.
Решение: ![]() ;
;
![]()
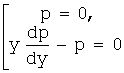
![]()
![]()
![]() ;
;

Заметим, что решение у=С получается из ![]() при С1=0.
при С1=0.
Следовательно, общее решение можно записать
в виде ![]() .
.
Замечание. Дифференциальные уравнения вида ![]() , не содержащие независимую переменную, допускают понижение
порядка на единицу, если положить
, не содержащие независимую переменную, допускают понижение
порядка на единицу, если положить ![]() , тогда
, тогда ![]()
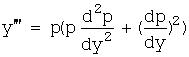 и т.д.
и т.д.
(формулы получены из правила
дифференцирования сложной функции).
Линейные
дифференциальные уравнения с постоянными коэффициентами (однородные и неоднородные)
Общее решение линейного однородного дифференциального уравнения с постоянными
коэффициентами ![]() (p,q – числа) может быть найдено с помощью
решения соответствующего характеристического
уравнения:
(p,q – числа) может быть найдено с помощью
решения соответствующего характеристического
уравнения: ![]() .
.
При этом:
-если
корни r1 и r2 характеристического
уравнения вещественны и r1 ¹ r2 , то общее решение имеет вид: ![]() ;
;
-если
корни r1 и r2 характеристического
уравнения вещественны и r1 = r2 = r, то общее решение имеет вид: ![]() ;
;
-если
корни r1 и r2 характеристического
уравнения комплексные ![]() ,
, ![]() , то общее решение имеет вид:
, то общее решение имеет вид: ![]() , где
, где ![]() ,
,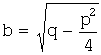 .
.
Во всех
трех случаях С1
и С2 – произвольные
постоянные.
17.Найти
решение дифференциального уравнения ![]() .
.
Решение.
Данное уравнение является линейным
однородным дифференциальным уравнением 2-го
порядка. Поэтому, для нахождения общего решения необходимо записать и решить
характеристическое уравнение ![]() .
.
Его корни
вещественны и различны: r1=1 и r2=4. Следовательно, общее
решение имеет вид: ![]() .
.
18.Найти решение дифференциального уравнения
![]() .
.
Решение. Характеристическое уравнение имеет
вид: ![]() .
.
Решением является
двукратный вещественный корень: r = 3.
Следовательно, общее решение данного уравнения: ![]() .
.
19.Найти решение
уравнения ![]() .
.
Решение.
Характеристическое уравнение имеет вид ![]() .
.
Поскольку дискриминант этого квадратного
уравнения отрицателен (D
= –1), то имеем случай комплексно-сопряженных корней. Решая, получим: r1 = 1 + i и r2
=
1 - i . Следовательно, общее решение
данного уравнения: ![]() .
.
Линейные неоднородные дифференциальные
уравнения с постоянными коэффициентами - это уравения
вида:
![]() , где p,q – числа, f(x)-непрерывная функция.
, где p,q – числа, f(x)-непрерывная функция.
Теорема (о структуре общего решения линейного
неоднородного уравнения). Если ![]() - общее решение линейного однородного уравнения, соответствующего
неоднородному линейному уравнению, а
- общее решение линейного однородного уравнения, соответствующего
неоднородному линейному уравнению, а ![]() - частное решение
линейного неоднородного уравнения, то их сумма
- частное решение
линейного неоднородного уравнения, то их сумма ![]() - общее решение линейного
неоднородного уравнения.
- общее решение линейного
неоднородного уравнения.
Отметим,
что в общем случае - найти частное решение неоднородного дифференциального
уравнения ![]() - это достаточно сложная задача. Рассмотрим её решение, когда правая часть уравнения f(x) имеет специальный вид (два случая:
I и II):
- это достаточно сложная задача. Рассмотрим её решение, когда правая часть уравнения f(x) имеет специальный вид (два случая:
I и II):
I. ![]() ,
,
где ![]()
![]()
-многочлен n-ой
степени.
В
этом случае частное решение ỹ находят следующим
образом:
1.Если α не совпадает ни с одним
из корней характеристического уравнения,
то ỹ ищется в виде ![]() ,
,
где
![]()
![]() (многочлен с
неопределёнными коэффициентами).
(многочлен с
неопределёнными коэффициентами).
2.Если α совпадает с одним из корней характеристического
уравнения,
то ỹ ищется в виде ![]() .
.
3.Если α совпадает с обоими
корнями характеристического уравнения, то ![]() .
.
В
случаях 2. и 3. говорят, что имеет место характеристический резонанс.
Для
вычисления коэффициентов многочлена Qn(x) используют метод неопределённых коэффициентов.
II.![]() , где b¹0; a;bÎR.
, где b¹0; a;bÎR.
В
этом случае с корнями характеристического уравнения сравнивают числа a±bi:
1.если a±bi – не совпадают с корниями
характеристического уравнения,
то частное решение ищут в
виде ![]() ,
,
где A, B – заранее
неизвестные числа, их находят методом неопределённых коэффициентов.
2.если a±bi – корни характеристического уравнения(резонанс),
то ![]() .
.
Замечание. Если ![]() и
и ![]() – частные решения уравнений
– частные решения уравнений ![]() и
и ![]() соответственно,
соответственно,
то
![]() – частное решение
уравнения
– частное решение
уравнения ![]() .
.
20.Найти решение дифференциального
уравнения ![]() .
.
Решение.
Решение соответствующего однородного уравнения было получено в примере 17.: ![]() =
= ![]() .
.
Исходя из вида правой части, найдем частное
решение неоднородного уравнения в виде: ![]() . Подставляя это решение в исходное дифференциальное
уравнение, получим:
. Подставляя это решение в исходное дифференциальное
уравнение, получим:
![]() , т.е.:
, т.е.: ![]() ,
,
откуда следует, что: ![]() . Поскольку общее решение неоднородного линейного уравнения может
быть найдено как сумма общего интеграла соответствующего однородного уравнения
и частного решения неоднородного уравнения, окончательно получим:
. Поскольку общее решение неоднородного линейного уравнения может
быть найдено как сумма общего интеграла соответствующего однородного уравнения
и частного решения неоднородного уравнения, окончательно получим: ![]() .
.
21.Найти общее решение уравнения ![]() .
.
Решение. Общее решение имеет вид ![]() ,
,
где
![]() - общее решение соответствующего однородного уравнения:
- общее решение соответствующего однородного уравнения:
![]() ,
, ![]() - частное решение данного уравнения.
- частное решение данного уравнения.
Решаем
сначала ![]() .
.
Характеристическое
уравнение ![]() ,
,
![]() ;
; ![]() =>
=> ![]() ;
;
Правая
часть ![]() ;
;
![]() ,
, ![]() =>
=> ![]() ,
,
где
![]() – многочлен первой степени,
– многочлен первой степени,
A и B
– неопределённые коэффициенты, их нужно найти.
Для
этого ![]() ,
,![]() подставим в
подставим в ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
,
![]()
![]()
![]()
Приравнивая
коэффициенты при одинаковых степенях х, получим:
![]() при x1 :
-2A=1
Решаем эту систему:
при x1 :
-2A=1
Решаем эту систему:
при
x0 :
2A-B=0 A=-0.5; B=-1.
=>
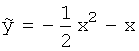
=>
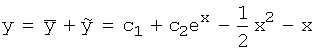
-
общее решение исходного уравнения.
22.Найти общее решение уравнения ![]()
Решение.
Найдем
корни характеристического уравнения ![]() ,
,
тогда
 ,
,
следовательно
![]() ,
, ![]() ,
,
тогда
общее решение однородного уравнения будет иметь вид ![]()
Представим
правую часть уравнения, как ![]()
и
сравним с выражением, задающим правую часть специального вида ![]() ,
,
т.к.
![]()
-
многочлен второй степени, то общий вид частного решения ![]() .
.
![]() ,
, ![]() ,
, ![]()
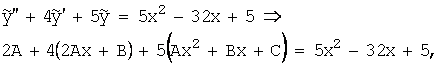
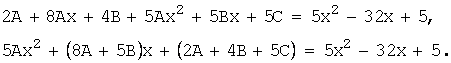
Сравнивая коэффициенты при соответствующих степенях ![]() слева и справа, найдем
слева и справа, найдем ![]() , решив систему:
, решив систему:
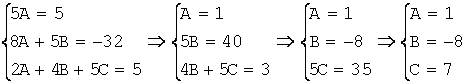 , отсюда
, отсюда ![]() .
.
Тогда общее решение заданного
неоднородного линейного уравнения имеет вид: ![]() .
.
23.Найти общее решение уравнения ![]() .
.
Решение:
Решим
сначала соответствующее однородное уравнение ![]() .
.
Характеристическое
уравнение r2+4=0,r1,2= ± 2i,
![]() – общее решение
однородного уравнения.
– общее решение
однородного уравнения.
Правая
часть ![]() ,
,
a = 0; b = 3; a
± bi = ± 3i ¹ ± 2i,
значит ![]() .
.
A и B
ищем методом неопределенных коэффициентов
![]() ,
, ![]() .
.
Подставляем
![]() и
и![]() в исходное уравнение
в исходное уравнение
![]() .
.
Приравниваем
коэффициенты соответственно при cos3x и sin3x в левой и правой
частях равенства:
![]() При cos3x:
-9A+4A=1
При cos3x:
-9A+4A=1
При sin3x:
-9B+4B=0 Þ A=![]() , B=0 .
, B=0 .
Т.о.,
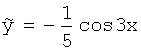 .
.
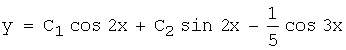 .
.
24.Решить
уравнение ![]() .
.
Решение:
Сначала
решим соответствующее однородное уравнение ![]() .
.
Характеристическое
уравнение r2-r-2=0 имеет корни
r1 = -1; r2 = 2 => y = ![]() = C1e-x + C2e2x.
= C1e-x + C2e2x.
Для
нахождения частного решения ![]() рассмотрим два
уравнения
рассмотрим два
уравнения
![]() и
и ![]() .
.
По
виду правой части найдем соответствующие частные решения этих уравнений:
![]() ;
; ![]() (вычисления опущены).
(вычисления опущены).
Тогда
![]() и
и
![]()
– общее решение данного
уравнения.