КРИВЫЕ ВТОРОГО ПОРЯДКА

Алгебраической кривой второго порядка называется кривая, уравнение которой в декартовой системе координат имеет вид:

Аx² + 2Вxy + Сy² + 2Dx + 2Еy + F = 0,

где не все коэффициенты А, В и С равны одновременно нулю, т.е. .

Если кривая невырожденная, то для неё найдется такая декартова прямоугольная система координат, в которой уравнение этой кривой примет один из следующих трех видов (каноническое уравнение):

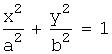, a>0,b>0 - эллипс,

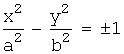, a>0,b>0 - гипербола,

px - парабола.

Окружность радиуса R с центром в начале координат будем рассматривать как частный случай эллипса.

Прежде чем рассматривать приведение общего уравнения линии второго порядка к его простейшим каноническим формам, остановимся на изучении геометрических свойств перечисленных кривых.

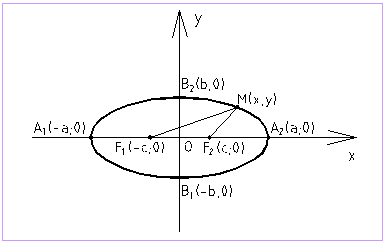
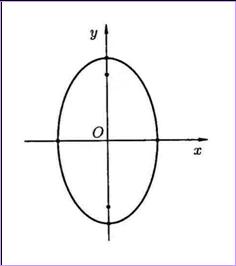
Эллипс – множество точек плоскости, сумма расстояний от которых до двух точек и , называемых фокусами, есть величина постоянная 2a, большая, чем расстояние между фокусами 2c: .

Эллипс, заданный каноническим уравнением: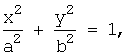

симметричен относительно осей координат. Параметры а и b называются полуосями эллипса (большой и малой соответственно), точки , , , называются его вершинами.

Если а>b, то фокусы находятся на оси ОХ на расстоянии от центра эллипса О.

Число ()

называется эксцентриситетом эллипса и является мерой

его «сплюснутости»

(при эллипс является окружностью:

= a² = b²).

Если а<b, то фокусы находятся на оси ОY и ,

().

Гипербола – множество точек плоскости, модуль разности расстояний от которых до двух точек и , называемых фокусами, есть величина постоянная 2a, меньшая, чем расстояние между фокусами 2c: .

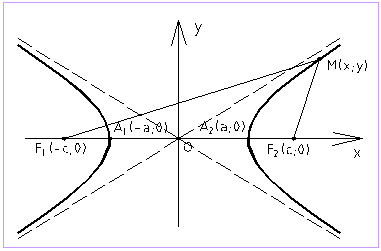Гипербола, заданная каноническим уравнением:

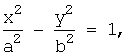
симметрична относительно осей координат. Она пересекает ось ОХ в точках и - вершинах гиперболы, и не пересекает оси ОY.

Параметр а называется действительной (вещественной) полуосью, b – мнимой полуосью.

Число , ()

называется эксцентриситетом гиперболы.

Прямые называются асимптотами гиперболы.

Гипербола, заданная каноническим уравнением:

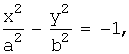
(или ),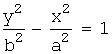

называется сопряжённой (имеет те же асимптоты). Её фокусы расположены на оси OY. Она пересекает ось ОY в точках и - вершинах гиперболы и не пересекает оси ОX.

В этом случае параметр b называется действительной (вещественной) полуосью, a – мнимой полуосью. Эксцентриситет вычисляется по формуле: , ().

Парабола – множество точек плоскости, равноудаленных от данной точки F, называемой

фокусом, и данной прямой, называемой директрисой: .

Парабола, заданная указанным каноническим уравнением, симметрична относительно оси ОХ.

Уравнение задает параболу, симметричную относительно оси ОY.

Парабола имеет фокус и директрису .

Парабола имеет фокус и директрису .

Если р>0, то в обоих случаях ветви параболы обращены в положительную сторону соответствующей оси, а если р<0 – в отрицательную сторону.

Примеры решения задач.

1.Написать каноническое уравнение гиперболы с фокусами на оси ОХ, зная что:

а) расстояние между фокусами 2c=30, а между вершинами 2a=20;

б) вещественная полуось равна 5, эксцентриситет .

Решение:

а) по условию ; ; ; ;

из соотношений . Ответ: .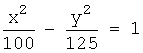

б) по условию ; , .

Ответ: .

2. Написать уравнение параболы, зная, что:

а) парабола проходит через точки (0,0); (3,6) и симметрична относительно оси ОХ,

б) парабола проходит через точки (0,0); (4,2) и симметрична относительно оси ОY.

Решение:

а)

Точка (3,6) лежит на параболе, поэтому ,

- уравнение директрисы

- уравнение параболы

б)

Точка (4,2) лежит на параболе, поэтому

- уравнение директрисы,

- уравнение параболы.

Приведение к каноническому виду общего уравнения кривой второго порядка

Рассмотрим в декартовой прямоугольной системе координат Oxy уравнение второго порядка общего вида:

Аx² + 2Вxy + Сy² + 2Dx + 2Еy + F = 0,

где не все коэффициенты А, В и С равны одновременно нулю.

Оно задаёт кривую второго порядка.

Наша цель: поменять систему координат так, чтобы максимально упростить данное уравнение.

Для этого сначала (если B0) повернём искодный базис (координатные оси Ox и Oy) на угол α против часовой стрелки таким образом, чтобы новые оси Ox’ и Oy’ стали параллельны осям кривой, при этом исчезнет слагаемое 2Вxy:

,

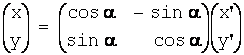где -

матрица линейного преобразования: поворот на угол α против часовой стрелки.

Или, наоборот, .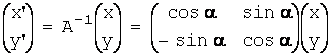

A(x’cosα - y’sinα)² + 2B(x’cosα - y’sinα)(x’sinα + y’cosα)+

+ C(x’sinα + y’cosα)² + 2D(x’cosα - y’sinα) +

+ 2E(x’sinα + y’cosα) + F = 0

Приведём подобные и выберем угол α так, чтобы коэффициент при произведении x’y’ обратился в ноль, т.е. чтобы выполнялось равенство

-2Acosαsinα + 2B(cos²α - sin²α) + 2Csinαcosα = 0

или

или

В новой системе координат Ox’y’ (после поворота на угол α), учитывая, что

; ,

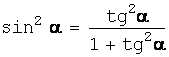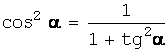уравнение будет иметь вид

А’x’² + С’y’² + 2D’x’ + 2Е’y’ + F’ = 0,

где коэффициенты А’ и С’ не равны одновременно нулю.

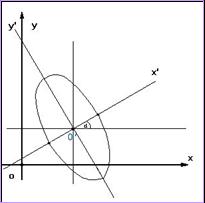
Следующий этап упрощения заключается в параллельном переносе осей Ox’ и Oy’ до совпадения их с осями кривой, при этом начало координат совпадёт с центром (или вершиной, в случае параболы) кривой. Техника преобразований на данном этапе заключается в выделении полного квадрата.

Таким образом, мы получим канонические уравнения кривых второго порядка.

Всего возможны 9 качественно различных случаев (включая случаи вырождения и распадения):

1. 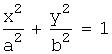(эллипс),

2. 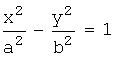(гипербола),

3. px (парабола),

4. 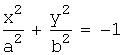(мнимый эллипс),

5. (пара мнимых параллельных прямых),

6. (пара параллельных прямых),

7. (пара совпавших прямых),

8. (точка (пара мнимых пересекающихся прямых)),

9. (пара пересекающихся прямых).

Рассмотрим пример.

Записать классическое уравнение гиперболы в канонической форме. Сделать чертёж.

Решение.

yx-1=0,

сделаем замену переменных:

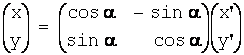, тогда

(x’cosα - y’sinα)(x’sinα + y’cosα)-1 = 0,

x’²cos²α - y’²cosαsinα + x’y’(cos²α - sin²α) – 1 = 0,

(cos²α - sin²α) = 0

.

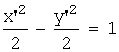Совершенно аналогично, каноническое уравнение для гиперболы

будет иметь вид: или .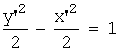

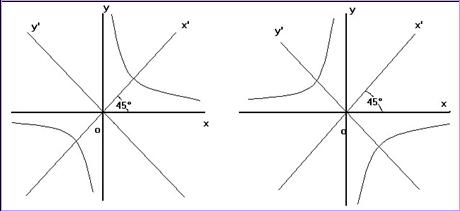
Отметим, что существует строгая математическая теория приведения кривых второго порядка (квадратичных форм) к каноническому виду. В частности, рассматриваются инварианты общего уравнения линии второго порядка по отношению к преобразованию одной декартовой системы координат в другую:

I₁ = A+C, I₂ = 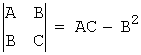, I₃=,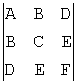

т.е. выражения, которые остаются неизменными при параллельном переносе и повороте осей координат.

В зависимости, например, от знака инварианта I₂ линии второго порядка классифицируются по следующим трём типам:

1)эллиптический, при ;

2)гиперболический, при ;

3)параболический, при .

Найдя корни характеристического уравнения

:,

сразу можно записать канонический вид эллипса

или гиперболы: .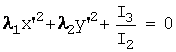

Для параболы каноническое уравнение будет выглядеть так: .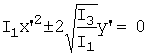

Кривые 2-го порядка со смещёнными центрами (вершинами)

Если в общем уравнении кривой 2-го порядка

,

в частности В = 0, то есть отсутствует член с произведением переменных, то это означает, что оси кривой параллельны координатным. Рассмотрим уравнение:

(A и C одновременно). Можно показать, что при этом:

1) Если АС > 0 (коэффициенты при квадратах переменных одного знака), то уравнение определяет эллипс;

2) Если АС < 0 (коэффициенты при квадратах переменных имеют разные знаки), то уравнение определяет гиперболу;

3) Если АС = 0 (один из членов с квадратом переменных отсутствует), то этим уравнением определяется парабола.

В каждом из случаев 1), 2), 3) могут встретиться вырожденные кривые, которыми мы заниматься не будем.

Для того чтобы понять, как именно расположена кривая относительно системы координат и каковы ее параметры, уравнение можно преобразовать способом выделения полных квадратов. После этого уравнение примет вид одного из невырожденных уравнений кривой 2-го порядка со смещенным центром:

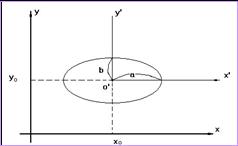
1)

это уравнение эллипса с центром и осями, параллельными осям и ;

Окружность радиуса R с центром в точке :

будем рассматривать как частный случай эллипса.

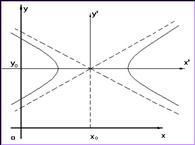
2)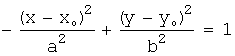 и ,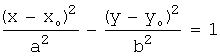

эти уравнения определяют гиперболы с центром и осями, параллельными координатным;

3)

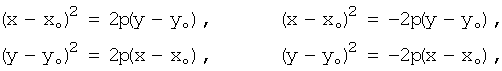
это параболы с вершиной и осью, параллельной одной из координатных.

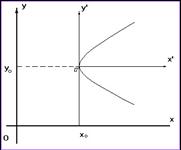
Примеры решения задач.

Определить вид кривой, найти ее центр (вершину) и вычислить основные параметры:

1)

2)

Решение примера 1:

Так как А=9, С= - 4, т.е. АС<0, то это уравнение определяет гиперболу. Преобразуем уравнение. Объединяем члены с одной переменной, коэффициент при квадрате выносим за скобку:

Дополняем выражения в скобках до полных квадратов:

Лишние свободные члены из скобок убираем и переносим вправо, тождественно преобразуя левую часть:

или

Делим на (-36):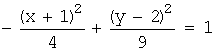

получили гиперболу с центром , полуосями a=2, b=3, осями параллельными координатным.

Действительная ось гиперболы параллельна оси : x= -1:

мнимая – параллельна оси : y=2; .

Фокусы:

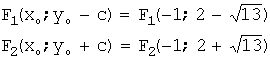
Асимптоты гиперболы:

Решение примера 2:

Так как С = 0, то уравнение определяет параболу с осью параллельной оси , т.е. уравнение должно быть преобразовано к одному из видов:

Преобразуем уравнение:

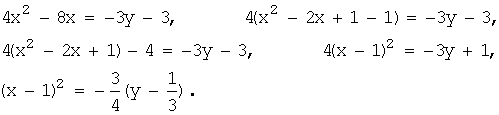
Вершина параболы

Ось x = 1 – параллельна оси .

Ветви направлены вниз, параметр .

Фокус:

Директриса: .

Эллипс, гипербола и парабола как конические сечения

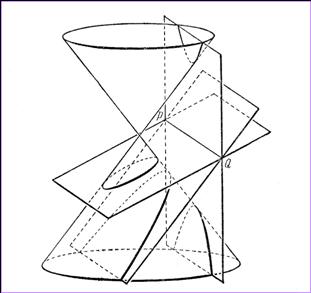Теорема.

Сечением любого круглого конуса плоскостью (не проходящей через его вершину) определяется кривая, которая может быть лишь эллипсом, гиперболой или параболой. При этом, если плоскость пересекает только одну полость конуса и по замкнутой кривой, то эта кривая есть эллипс; если секущая плоскость пересекает только одну полость конуса и по незамкнутой кривой, то эта кривая – парабола; если плоскость пересекает обе полости конуса, то в сечении образуется гипербола.

Справедливость этой теоремы можно установить, исходя из того общего положения, что пересечение поверхности второго порядка плоскостью есть линия второго порядка.

Из рисунка видно, что, поворачивая секущую плоскость вокруг прямой PQ, мы меняем кривую сечения. Будучи, например, первоначально эллипсом, она на одно мгновение становится параболой, а затем превращается в гиперболу. Параболой эта кривая будет тогда, когда секущая плоскость параллельна касательной плоскости конуса.

Заметим, что уравнение конуса второго порядка имеет вид: .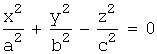

Таким образом, эллипсы, гиперболы и параболы называются коническими сечениями.