НЕОПРЕДЕЛЁННЫЙ
ИНТЕГРАЛ
Функция F(x) называется первообразной функцией (или просто первообразной) для заданной
функции f(x) на интервале (а,b),
если в любой точке x этого
интервала функция F(x) дифференцируема и имеет
производную F’(x), равную f(x), т.е. ![]() .
.
Если F(x)
является первообразной для функции f(x) на интервале (a,b), то,
очевидно, и функция F(x)+C , где С
– любая постоянная (константа), является первообразной для функции f(x) на
интервале (a,b).
Неопределённым интегралом от функции f(x) называется совокупность всех
её первообразных и обозначается
![]() ,
,
где f(x)
называется подынтегральной функцией, f(x)dx – подынтегральным
выражением.
Отыскание
неопределённого интеграла называется интегрированием функции.
Основные
свойства неопределённого интеграла
![]()
![]()
![]()
![]() где А=const.
где А=const.
![]()
Таблица
основных неопределённых интегралов
1.![]() 2.
2. ![]()
3. 4.
4.![]()
5.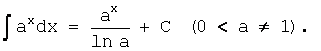 6.
6.![]()
7.![]() 8.
8.![]()
9.![]()
10.![]()
11.
12.
13.![]()
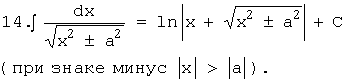
Отметим,
что интегралы от некоторых элементарных функций
уже не являются элементарными функциями. Примерами таких интегралов
могут служить следующие:
1.![]()
![]() интеграл Пуассона, широко используется в статистической
физике, математической статистике, теории теплопроводности и диффузии.
интеграл Пуассона, широко используется в статистической
физике, математической статистике, теории теплопроводности и диффузии.
2.Интегралы ![]() , называемые интегралами Френеля, широко применяются в
оптике.
, называемые интегралами Френеля, широко применяются в
оптике.
Часто встречается в приложениях интегральный
логарифм
3.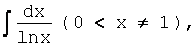
а также интегральные синус
и косинус:
4.![]()
5.![]()
Методы
интегрирования
В зависимости от вида подынтегральной функции применяются различные
методы интегрирования.
1. Непосредственное
применение табличных формул
интегрирования и свойств интеграла
В наиболее простых случаях интегрирование осуществляется либо непосредственным применением табличных формул,
либо после простых алгебраических преобразований подынтегрального выражения.
Например, используя формулу 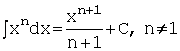 , получим:
, получим:
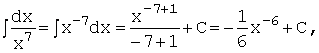
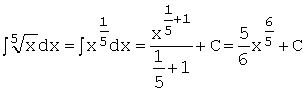 ,
,
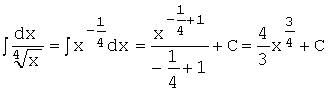 ,
,
а применяя
табличную формулу интегрирования 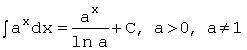 , получим:
, получим:
 .
.
Используя свойства
неопределенного интеграла и табличные формулы
интегрирования:
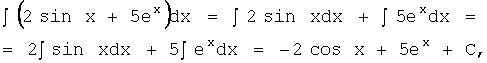
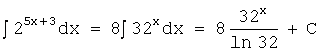 ,
,
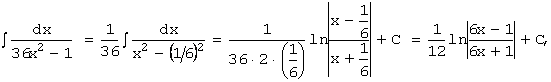
![]()
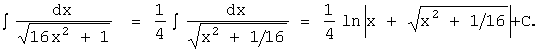
2.Метод
замены переменной
Метод замены переменной (или метод подстановки) основан на
применении следующей формулы: ![]() .
.
Например:

Частным случаем метода замены переменной является использование
линейной подстановки: ![]() . В этом случае справедлива следующая формула:
. В этом случае справедлива следующая формула: ![]() .
.
Например: ![]()

![]() .
.
Метод подведения
под знак дифференциала
Метод
подведения под знак дифференциала основан на следующих свойствах дифференциала
функции:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
3.Метод интегрирования по частям
Исходное подынтегральное выражение разбивают на два сомножителя u и dv, и далее применяют формулу ![]() .
.
Аналитические выражения для v и du (которые
подставляются в интеграл правой части равенства) вычисляют так: du
находится путем дифференцирования функции u=u(x) (![]() ), функция v(x) находится путем интегрирования dv (
), функция v(x) находится путем интегрирования dv (![]() ,С=0).
,С=0).
Применение данного метода
дает положительные результаты в случае, если интеграл, стоящий в правой части
формулы оказывается более “простым”, чем исходный (стоящий в левой). В частности, его полезно
применять в следующих случаях:
1)подынтегральная
функция содержит произведение многочлена от x на показательную функцию от x, на sinx или cosx, или произведение
многочлена от x
на lnx;
2)
подынтегральная функция представляет собой одну из обратных тригонометрических
функций arcsinx,
arccоsx и т.д.;
3) подынтегральная функция есть
произведение показательной функции на sinx, cosx или
многочлен от x.
В некоторых случаях однократного применения
формулы интегрирования по частям оказывается недостаточным, тогда результат
достигается путём ее многократного применения.
Как именно
разбить подынтегральное выражение на u и dv, ориентирует
следующая подсказка (хотя с увеличением опыта интегрирования, это становится
очевидным):
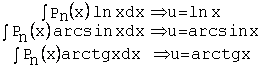
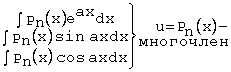
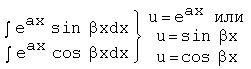
4. Интегрирования рациональных дробей
Целой рациональной функцией (многочленом
степени n) называется выражение вида:
![]() ,
,
где ![]() - действительные числа,
- действительные числа, ![]() .
.
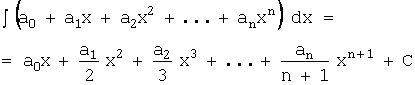
Дробной
рациональной функцией (рациональной дробью)
называется отношение двух многочленов:
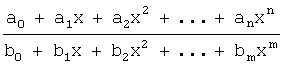 .
.
Правильной называется дробь, у которой
степень числителя меньше степени знаменателя (m<n), неправильной – (m³n).
Используя алгоритм деления многочленов (деление ‘столбиком’), любую неправильную рациональную дробь
можно представить в виде алгебраической суммы многочлена и правильной дроби.
Например, пусть дана неправильная дробь:
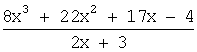 .
.
Поделим числитель на знаменатель:
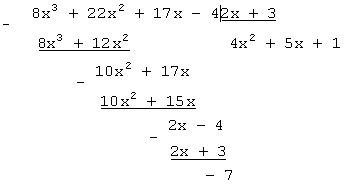
Таким образом, неправильная дробь 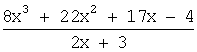
может быть представлена
в виде алгебраической суммы многочлена ![]() и правильной дроби
и правильной дроби ![]() :
:
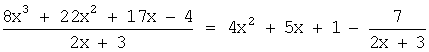 .
.
Соответственно интеграл от рациональной дроби 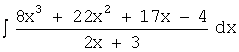
может быть представлен
в виде суммы двух интегралов:
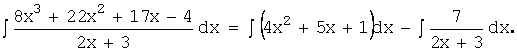
Интегрирование
правильных дробей
Интегрирование правильных дробей сводится к
интегрированию простейших дробей.
1.![]() .
.
2. 
3.![]()
а) Дискриминант равен нулю (D=0). В этом случае, квадратный трехчлен может быть записан как ![]() ,
,
где ![]() - корень квадратного
уравнения
- корень квадратного
уравнения
![]() .
.
Таким
образом:
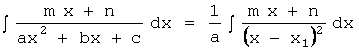 =
=

![]() .
.
б) Значение дискриминанта - положительно (D>0).
В этом случае: ![]() ,
,
где ![]() и
и ![]() - корни квадратного
уравнения
- корни квадратного
уравнения ![]() .
.
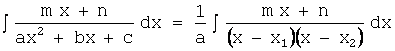 .
.
Представим
подынтегральную функцию в виде суммы двух слагаемых: 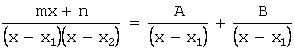 .
.
Найдем значения неопределённых коэффициентов А и В:

т.е. 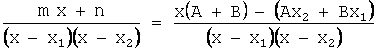 .
.
Приравнивая коэффициенты при x
и свободные члены, получим систему уравнений
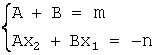 ,
,
решая которую, найдем значения А и В. Далее, подставляя полученные значения, выполним
интегрирование:
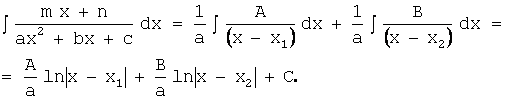
в) Значение дискриминанта - отрицательно (D<0). Выделим полный квадрат в
знаменателе:
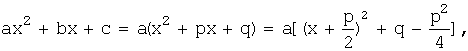
причём q-![]() >0.
Обозначим q-
>0.
Обозначим q-![]() =s2 и сделаем замену переменной
x+
=s2 и сделаем замену переменной
x+![]() =t, тогда x = t-
=t, тогда x = t-![]() , dx=dt:
, dx=dt:
![]()

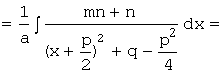
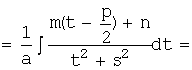
![]()
![]()
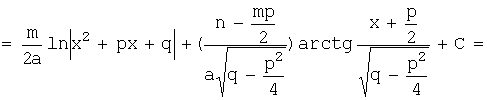
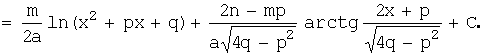
Отметим, что ![]()
5.Интегрирование рациональных функций
Интегрирование выражений вида ![]() , где подынтегральная функция
, где подынтегральная функция ![]() является рациональной
функцией от
является рациональной
функцией от ![]() , производится методом замены
переменной:
, производится методом замены
переменной: ![]() ,
,![]() и
и ![]() .
.
Интегрирование выражений вида ![]() , где подынтегральная функция
, где подынтегральная функция ![]() является рациональной
функцией от
является рациональной
функцией от ![]() и
и ![]() , производится методом замены переменной (универсальная
тригонометрическая подстановка):
, производится методом замены переменной (универсальная
тригонометрическая подстановка):![]() ,(
,(![]()
 ,
, 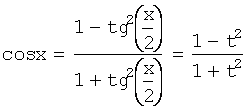 ,
,
![]() ,
, 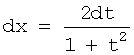 .
.
6.Интегрирование
некоторых иррациональных функций
Интегрирование иррациональных функций, в общем случае, представляет
достаточно сложную задачу.
1. Интеграл вида ![]() , где R –
рациональная функция, и
, где R –
рациональная функция, и ![]() ,
, ![]() , … - рациональные числа приводится к интегралу от
рациональной функции путем подстановки
, … - рациональные числа приводится к интегралу от
рациональной функции путем подстановки ![]() , где: k – общий знаменатель
всех дробных показателей степеней x.
, где: k – общий знаменатель
всех дробных показателей степеней x.
2. К интегралам от функций,
рационально зависящих от тригонометрических функций, сводятся интегралы:
![]() - подстановкой
- подстановкой ![]() ;
;
![]() - подстановкой
- подстановкой ![]() ;
;
![]() - подстановкой
- подстановкой ![]() ;
;
7.Интегрирование
тригонометрических функций
При интегрировании выражений:
а) ![]() ,
,
![]() ;
;
б) ![]() ;
;
в) ![]() ,
, ![]() ;
;
г) ![]() ,
, ![]() ,
, ![]() ,
,
где m и n –целые числа, полезны следующие
формулы:
![]() ;
; ![]() ;
;
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Примеры решения задач.
1.
Найти интеграл ![]() .
.
Используем свойства и табличную формулу
![]() :
:
![]()
 .
.
2.
Найти интеграл  .
.
Здесь для приведения к табличному виду
![]()
преобразуем подынтегральное выражение к сумме двух
слагаемых:

3.Найти
нижеследующие интегралы, используя метод подведения под знак дифференциала:
а) ![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)  .
.
Решение.
а) Учитывая, что ![]() и обозначив
и обозначив ![]() , получим:
, получим:
![]()
б)
Учитывая, что ![]() и, обозначив
и, обозначив ![]() , получим:
, получим:

в)Запишем исходное
выражение как: ![]() .
.
Заметив, что ![]() и, обозначив
и, обозначив ![]() , окончательно получим:
, окончательно получим:
![]()
г)Заметив, что: ![]() и обозначив
и обозначив ![]() , получим:
, получим:

4. Найти интеграл
![]() .
.
Здесь для применения табличной формулы 
необходимо преобразовать показатель степени
2x – 1. Сделаем подстановку: u = 2x – 1,
тогда du = 2dx и ![]() .
.

![]() .
.
5. Найти интеграл
![]() .
.

6. Найти интеграл ![]() .
.

![]()
7. Найти интеграл  .
.

![]()
![]() .
.
8. Найти интеграл ![]() .
.

![]() .
.
9. Найти интеграл ![]() .
.
Так как ![]() , то
, то
 .
.
10. Найти интеграл ![]() .
.
Приведем интеграл к табличному виду
![]() .
.

 .
.
11.Найти интегралы:
а)![]() ;б)
;б)![]() ;в)
;в)![]() ; г)
; г)![]() ;д)
;д)![]() ;е)
;е)![]() ;
;
ж)![]() .
.
а)Подынтегральная
функция содержит произведение многочлена от x (первой степени) на sinx.
Разобьем подынтегральное выражение на две части u и dv,
положив u = x, dv = sinxdx, найдем du и v как: ![]() и
и ![]() , т.е: du = dx,
, т.е: du = dx,
и ![]() .
.
Далее, применим формулу интегрирования
по частям ![]() :
:

б)Аналогично,

в)Разобьем
подынтегральное выражение на две части u и dv,
положив u = lnx, dv = xdx. Найдем du и v как: ![]() ,
,
и ![]() .
.

г)аналогично,

д)Положив u =(2x +1), ![]() , найдем du и v: :
, найдем du и v: : ![]() ,
,
и ![]() .
.

е)Разобьем
подынтегральное выражение на две части u и dv,
положив ![]() , dv = sinxdx. Найдем du и v:
, dv = sinxdx. Найдем du и v: ![]() ,
, ![]() ,
,
![]() .
.
Хотя окончательный результат и не
получен, однако достигнуто определенное упрощение
исходного интеграла, т.к. понизилась степень многочлена подынтегрального выражения.
Поэтому применим данную формулу повторно.
Вновь разбив
подынтегральное выражение на две части u и dv
и, положив ![]() , dv = cosxdx, найдем du и v:
, dv = cosxdx, найдем du и v: ![]() ,
,
![]() .
.
Повторно применим формулу интегрирования
по частям:

Подставляя полученное выражение, окончательно получим:

ж)Положив ![]() ,
, ![]() , найдем du и v:
, найдем du и v: ![]() ,
,
![]() ,
,
![]() .
.
Поскольку конечный результат достигнуть не удалось,
вновь применим метод интегрирования по частям,
положив ![]() ,
, ![]() . Тогда
. Тогда ![]() ,
,
![]() ,
,
![]() .
.
Подставляя,
получим:
![]() .
.
Откуда:

12. Найти интеграл ![]() .
.
В случае, когда нужно найти интеграл от неправильной
дроби (когда степень числителя больше или равна степени знаменателя),
используют прием деления «столбиком».
|
Разделим: |
|
2x – 1 |
x+1 |
,
следовательно |
|
|
|
2x + 2 |
2 |
|
|
|
|
–3 |
|
|
![]() .
.
Тогда:

13. Найти интеграл ![]()
Делим:
|
|
x3 + 0 + x + 0 |
–x + 1 |
|
|
||||||
|
|
x3 - x2 |
–x2 – x – 2 |
|
|||||||
|
|
x2 +x |
|
|
|
||||||
|
|
x2 –x |
|
|
|
||||||
|
|
2x + 0 |
|
|
|
||||||
|
|
2x – 2 |
|
|
|
||||||
|
|
2 |
|
|
|
||||||
Таким
образом: ![]() , откуда
, откуда

 .
.
14. Найти интеграл ![]() .
.
Если
знаменатель дроби разлагается на простые множители (x – xi), то
для интегрирования таких дробей используется метод неопределенных
коэффициентов:
 .
.
Так
как ![]() , то
, то
![]() .
.
Приведем
правую часть к общему знаменателю:
![]() .
.
Т.к. знаменатели справа и слева совпадают,
приравняем числители, и, раскрывая скобки, получим: ![]() .
.
Чтобы два алгебраических выражения были тождественно
равны, необходимо приравнять коэффициенты при соответствующих степенях.
Получаем систему уравнений:
 . Отсюда
. Отсюда ![]() ;
; ![]() и
и
![]() .
.
Таким
образом,
![]()
![]() .
.
15. Найти интеграл ![]() .
.
Аналогично
предыдущему примеру, имеем:
![]() ;
;
![]() ;
;
![]() .
.
Соответствующая
система уравнений и ее решение:
 .
.
Таким
образом,
![]()
![]() .
.
16. Найти интеграл ![]() .
.
Здесь
дискриминант знаменателя ![]() , поэтому разложить знаменатель на множители не удается. Например,
можно использовать формулу:
, поэтому разложить знаменатель на множители не удается. Например,
можно использовать формулу:
![]()

В
нашем случае ![]() . После подстановки и вычислений получим:
. После подстановки и вычислений получим: ![]()
17.Найти интеграл
 .
.
Вводя обозначение ![]() , и учитывая, что
, и учитывая, что ![]() и
и ![]() , получим:
, получим:

18.
Найти интеграл: 
Положим ![]() , тогда
, тогда ![]() , подставляя, получим:
, подставляя, получим:

19.Найти интегралы:
а) ![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)![]() ;
;
Решение.

б)отделяем от нечетной степени один множитель:
![]() , и делаем замену переменной:
, и делаем замену переменной: ![]() ,
, ![]() .
.
Подставляя, получим:

в)Полагаем: ![]() . Тогда:
. Тогда: ![]() и
и ![]() .
.
Подставляя, получим:

г)Разлагаем подынтегральную
функцию на слагаемые и затем интегрируем:

.