НЕСОБСТВЕННЫЙ ИНТЕГРАЛ

Ранее, при рассмотрении определенного интеграла , предполагалось, что:

а) областью интегрирования служит конечный промежуток ;

б) подынтегральная функция ограничена(непрерывна) на этом промежутке.

Если эти условия не выполнены, рассматривают так называемые несобственные интегралы (первого и второго рода):

первого рода - от непрерывной функции по бесконечному промежутку интегрирования; второго рода - по конечному промежутку интегрирования, но от неограниченной функции.

Несобственный интеграл по бесконечному промежутку интегрирования

Пусть функция определена на бесконечном промежутке и интегрируема на произвольном конечном отрезке , где . Рассмотрим функцию , как интеграл с переменным верхним пределом: , .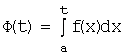

Определение. Несобственным интегралом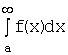

от функции на бесконечном промежутке называется предел, к которому стремится функция при t, стремящемся к , т.е.: .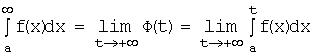

Если рассматриваемый предел существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), а величина этого предела – I называется значением несобственного интеграла: .

В противном случае – несобственный интеграл называется расходящимся.

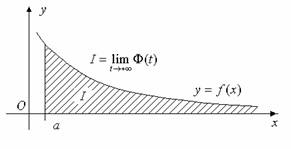
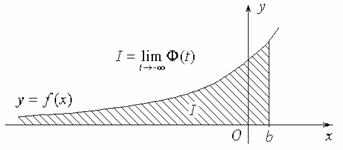
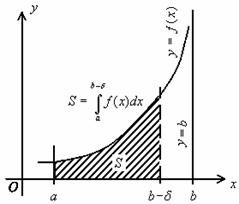
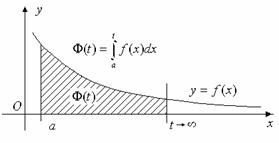Геометрическая интерпретация. Рассмотрим неотрицательную функцию , которая определена на бесконечном промежутке и интегрируема на произвольном конечном отрезке , где .

Геометрически значение функции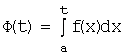

численно равно площади области, ограниченной отрезком оси Ox (), графиком функции и отрезками прямых и .

Сходящимся несобственным интегралам геометрически соответствуют неограниченные области, площадь которых конечна.

Несобственный интеграл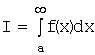

численно равен площади неограниченной области, лежащей в координатной плоскости выше луча оси Ox и ниже графика функции .

Расходящиеся интегралы (для ) соответствуют неограниченным областям с бесконечной площадью. В случае, когда при , пишут формально: .

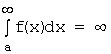По аналогии с несобственными интегралами на полуинтервале определяется несобственный интеграл на полуинтервале :

.

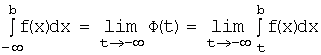Если рассматриваемый предел существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), а величина этого предела – I называется значением несобственного интеграла:.

В противном случае – несобственный интеграл называется расходящимся.

Аналогична и геометрическая интерпретация: несобственный интеграл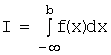

характеризует площадь неограниченной области, ограниченной лучом оси Ox и графиком функции .

Коснёмся также понятия несобственного интеграла с двумя бесконечными пределами, на интервале , который определяется формулой: ,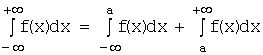

где а-произвольное число.

Несобственный интеграл 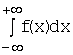называется сходящимся,

если сходятся оба интеграла 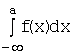и .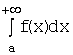

Если же хотя бы один из интегралов расходится, то интеграл 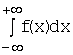называется расходящимся.

Заметим, что определение несобственного интеграла на бесконечном интервале не зависит от выбора числа a.

Примеры решения задач.

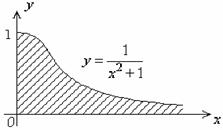
1.Вычислить значения несобственных интегралов: а) 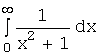; б) .

Решение.

а) Согласно определению, нам нужно вычислить .

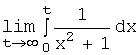Для этого определим функцию как: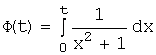

и найдем ее предельное значение при , т.е.: .

Применяя формулу Ньютона-Лейбница, получим: .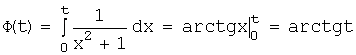

.

Таким образом: .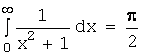

Для наглядности изобразим график подынтегральной функции .

б) Согласно определению, нам нужно вычислить .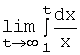

Для этого определим функцию как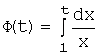

и найдем ее предельное значение при : .

Применяя формулу Ньютона-Лейбница, получим:

.

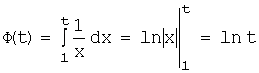Переходя к пределу, найдем что: .

Следовательно, искомый несобственный интеграл – расходится.

Несобственный интеграл от неограниченной функции

Пусть функция непрерывна и неограниченна на полуинтервале .

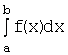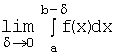Определение. Несобственным интегралом от непрерывной и неограниченной функции на полуинтервале называется предел , где: .

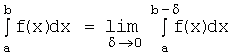Если рассматриваемый предел существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу). В противном случае – несобственный интеграл называется расходящимся и условно обозначается как: .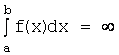

Аналогично определяется понятие несобственного интеграла от неограниченной непрерывной функции на полуинтервале .

Определение.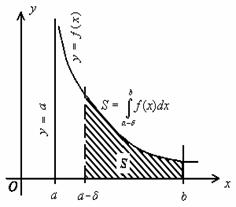 Несобственным интегралом 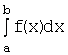от непрерывной и неограниченной функции на полуинтервале называется предел ,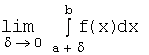

где : .

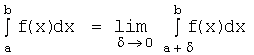Если рассматриваемый предел существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу). В противном случае несобственный интеграл называется расходящимся и условно обозначается .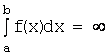

Примеры решения задач.

1.Найти площадь S фигуры, расположенной ниже графика функции 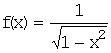на промежутке .

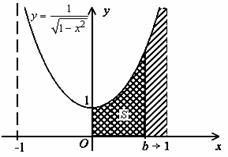Решение. Функция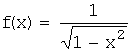

неограниченна на промежутке (стремится к при ) и неопределенна при .

Искомая площадь определяется несобственным интегралом .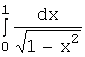

Возьмём произвольную точку b внутри заданного промежутка и вычислим определённый интеграл ,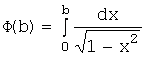

используя формулу Ньютона – Лейбница:

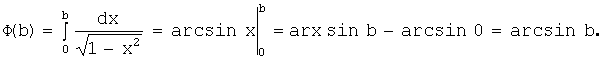
Переходя к пределу, получим: .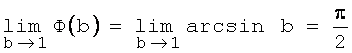

Таким образом, предел существует и конечен. Поэтому искомая площадь S, определяемая посредством сходящегося несобственного интеграла, равна .

2. Вычислить несобственный интеграл для: a) 0<p<1; б) p=1; в) p>1.

Решение. Нижний и верхний пределы интегрирования, а также область определения подынтегральной функции задают область интегрирования: .

При p>0 подынтегральная функция стремится к при , поэтому рассматриваемый пример соответствует случаю несобственного интеграла от неограниченной слева функции.

а)пусть 0<p<1, тогда .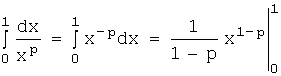

Учитывая, что согласно условию 0<p<1, получим, что величина 1-р (стоящая в знаменателе и показателе степени) положительна и меньше единицы, поэтому .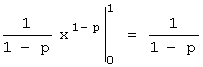

Т.е. при данном условии несобственный интеграл сходящийся и равен .

б)пусть p=1, тогда .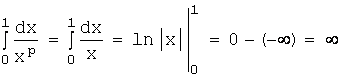

Таким образом, при данном условии несобственный интеграл расходится.

в)пусть p>1, тогда .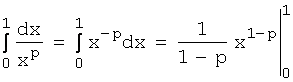

Согласно условию p>1, поэтому величина 1-р (стоящая в знаменателе и показателе степени) отрицательна. Из этого следует, что

.

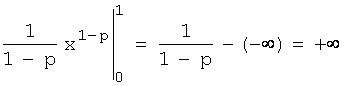Т.е. при данном условии несобственный интеграл расходится.

3.Как частные случаи предыдущего примера, рассмотрим значения: а) , б) .

Решение.

а) пусть , тогда ,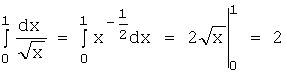

т.е. несобственный интеграл сходится.

б) пусть , тогда ,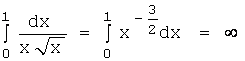

т.е. несобственный интеграл расходится.