ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Вектором
называется отрезок ![]() с указанным на нем направлением.
с указанным на нем направлением.
Обозначение: ![]() . Расстояние
. Расстояние ![]() называется длиной или
модулем вектора и обозначается
называется длиной или
модулем вектора и обозначается
![]() ;
; ![]() .
.
Коллинеарными
называются векторы, лежащие на одной прямой или на параллельных
прямых.
Компланарными называются векторы, расположенные в одной
или в параллельных плоскостях.
Базисом
на плоскости (в пространстве) называется пара (тройка) ненулевых неколлинеарных
(некомпланарных) векторов. Используется декартов (ортонормированный) базис –взаимоперпендикулярные
векторы единичной длины с общим началом (и одинаковым масштабом по всем осям).
Обозначается обычно: ![]() на плоскости,
на плоскости, ![]() в пространстве.
в пространстве.
Отметим, что ![]() ,
, ![]() ,
,![]() ,
,![]() .
.
Ортом оси называется вектор ![]() единичной длины
единичной длины ![]() =1, сонаправленный с осью.
=1, сонаправленный с осью.
Под
(координатной) осью будем понимать прямую OX
с выбранной на
ней точкой начала отсчёта O, направлением и масштабом
(единицей измерения длины).
Совокупность двух (трёх) взаимоперпендикулярных
осей с общим началом отсчёта и одинаковым масштабом по всем осям называется
декартовой (ортонормированной) системой координат на плоскости (в пространстве).
Оси
называются: Ox - ось абсцисс, Oy – ось ординат, Oz – ось
аппликат.
Пусть вектор ![]() (x,y,z)=
(x,y,z)= ![]() задан своими
декартовыми координатами, тогда его длина равна:
задан своими
декартовыми координатами, тогда его длина равна: ![]() =
= ![]()
Длина отрезка AB, где A(![]() ),
B(
),
B(![]() ) равна:
) равна: ![]() =
= ![]()
Рассмотрим
два вектора ![]() (
(![]() ) и
) и ![]() (
(![]() ) в декартовой системе
координат. Условие коллинеарности
) в декартовой системе
координат. Условие коллинеарности ![]() и
и ![]() запишется так:
запишется так: 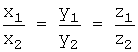 .
. ![]()
Скалярное
произведение![]() двух векторов
двух векторов ![]() и
и ![]() – это число, равное
произведению модулей этих векторов и косинуса угла между ними:
– это число, равное
произведению модулей этих векторов и косинуса угла между ними:
![]() ∙
∙![]() =
= ![]() ∙
∙![]() cos
cos![]()
![]() =
=
![]()
![]()
Условие перпендикулярности (ортогональности)
![]() и
и ![]() :
:![]() = 0.
= 0.
Векторным
произведением двух векторов ![]() и
и ![]() называется вектор
называется вектор ![]() =
= ![]()
![]()
![]() , обладающий следующими свойствами:
, обладающий следующими свойствами:
а) ![]() =
= ![]() ∙
∙![]() sin
sin![]() ,
где
,
где ![]() -угол между
-угол между ![]() и
и ![]() ;
;
б)
если ![]() и
и ![]() неколлинеарны,
то
неколлинеарны,
то ![]()
![]()
![]() и
и ![]()
![]()
![]() ;
;
в) ![]() ,
,![]() ,
,![]() образуют правую тройку.( Кратчайший поворот от
образуют правую тройку.( Кратчайший поворот от ![]() к
к ![]() виден из конца вектора
виден из конца вектора
![]() совершающимся против
часовой стрелки.)
совершающимся против
часовой стрелки.)
Вектор ![]() имеет координаты:
имеет координаты: ![]() =
= ![]()
![]()
![]() = =
= =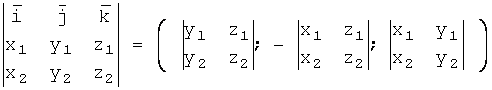 .
.
Если ![]() и
и ![]() неколлинеарны,
то
неколлинеарны,
то ![]() =
= ![]()
![]()
![]()
![]()
![]() численно равен площади параллелограмма, построенного на этих
векторах.
численно равен площади параллелограмма, построенного на этих
векторах.
Смешанным
произведением упорядоченной тройки векторов ![]() ,
,![]() ,
,![]() называется число,
равное скалярному произведению векторного произведения
называется число,
равное скалярному произведению векторного произведения ![]()
![]()
![]() и вектора
и вектора ![]() :
: ![]()
![]()
![]() =
= ![]()
![]()
![]() ∙
∙![]() =
=  .
.
Три ненулевых вектора ![]() ,
, ![]() ,
, ![]() компланарны
компланарны ![]()
![]()
![]()
![]() =0. Абсолютная величина смешанного произведения трёх
ненулевых некомпланарных векторов
=0. Абсолютная величина смешанного произведения трёх
ненулевых некомпланарных векторов ![]() ,
,![]() ,
,![]() равна объёму
параллелепипеда, построенного на этих векторах, как на рёбрах. Объём
соответствующей пирамиды равен
равна объёму
параллелепипеда, построенного на этих векторах, как на рёбрах. Объём
соответствующей пирамиды равен ![]() объёма
параллелепипеда.
объёма
параллелепипеда.
Примеры решения задач.
1.Даны точки А(1;2;3)
и В(-1;0;4). Найти модуль вектора ![]() и координаты точки Е – середины
отрезка
и координаты точки Е – середины
отрезка ![]() .
.
Решение: ![]() =( -1-1,0-2,4-3
),
=( -1-1,0-2,4-3
),
![]() =
= ![]() = 3,
= 3,
координаты
середины отрезка ![]() :
Е
:
Е![]() Е(0;1;3,5).
Е(0;1;3,5).
2. Найти орт вектора ![]() (-1;3;4).
(-1;3;4).
Решение: ![]() ,
,
![]() ,
,
![]() ,
,
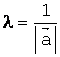 ,
,
![]() ,
следовательно,
,
следовательно,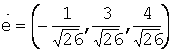 .
.
3. Найти проекцию вектора ![]() (3,4,5) на направление вектора
(3,4,5) на направление вектора ![]() (0;2;3).
(0;2;3).
Решение: .
.
4.Найти площадь треугольника
АВС, если известны координаты его вершин: А(1,-1,0), В(1,0,1), С(0,-1,2)
Решение: ![]()
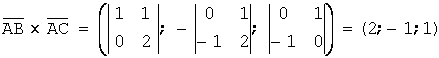 ,
,
![]()
![]()
![]() .
.
5. Найти площадь треугольника АВС, если
известны координаты его вершин: А(1,4), В(-2,1), С(1,1).
Решение: ![]() ,
,
![]() =(-3;-3)=(-3;-3;0),
=(-3;-3)=(-3;-3;0), ![]() =(0;-3)=(0;-3;0).
=(0;-3)=(0;-3;0).
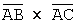 =
= 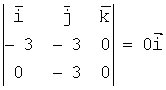 +
+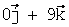 =(0;0;9),
=(0;0;9),
![]()
![]()
![]() .
.
6.Вычислить косинус угла между
векторами ![]() (2,0,-1) и
(2,0,-1) и ![]() (-3,1,0).
(-3,1,0).
Решение: 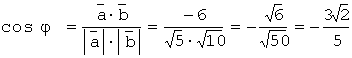 .
.